Kody Huffmana

by Jerry Sky

2020-10-29

1. Overview

X={x1,x2,…,xN}p1≥p2≥⋯≥pNX = \{x_1, x_2, \dots, x_N\} \quad p_1 \ge p_2 \ge \dots \ge p_N

  1. Budujemy las o drzewach jednoelementowych:

    ∘p1x1∘p2x2∘p3x3…∘pNxN. \underset{x_1}{\overset{p_1}{\circ}}\quad \underset{x_2}{\overset{p_2}{\circ}}\quad \underset{x_3}{\overset{p_3}{\circ}}\quad \dots\quad \underset{x_N}{\overset{p_N}{\circ}}.

  2. Wybieramy dwa drzewa o najmniejszych „wagach” i robimy z nich drzewo.

  3. Dostajemy las o drzewach:

    ∘p1x1∘p2x2…∘pN−2xN−2 \underset{x_1}{\overset{p_1}{\circ}}\quad \underset{x_2}{\overset{p_2}{\circ}}\quad \dots\quad \underset{x_{N-2}}{\overset{p_{N-2}}{\circ}} oraz
    .

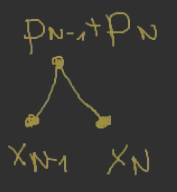  4. Sortujemy las względem „wag” i kończymy, jeśli zostało tylko jedno drzewo lub idziemy do kroku 1.

Na „dowidzenia” dostaniemy drzewo binarne (o wadze 11) i liściach etykietowanych {x1,x2,…,xN}\{x_1, x_2, \dots, x_N\}. Możemy z tego odczytać kody!

Gratis: owe kody są prefiksowe.

2. Przykład

Mamy

Czyli mamy las początkowy: ∘12x1∘13x2∘118x3∘118x4∘118x5. \underset{x_1}{\overset{\frac{1}{2}}{\circ}}\quad \underset{x_2}{\overset{\frac{1}{3}}{\circ}}\quad \underset{x_3}{\overset{\frac{1}{18}}{\circ}}\quad \underset{x_4}{\overset{\frac{1}{18}}{\circ}}\quad \underset{x_5}{\overset{\frac{1}{18}}{\circ}}.

Iterujemy:


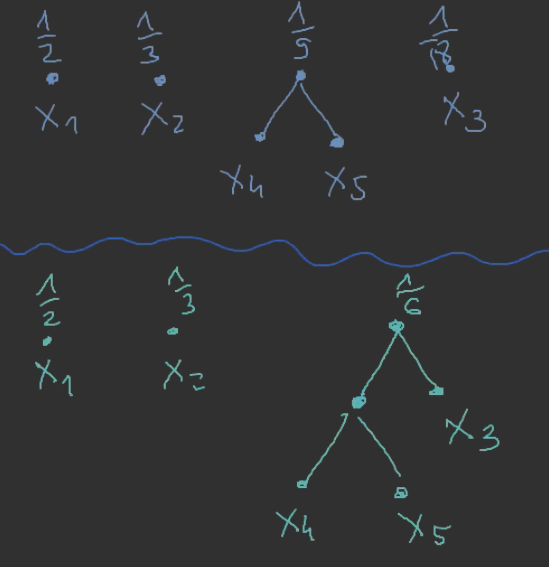
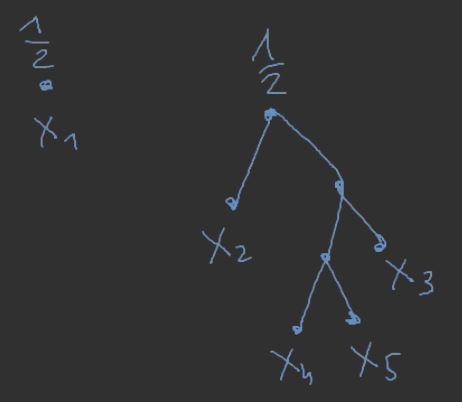
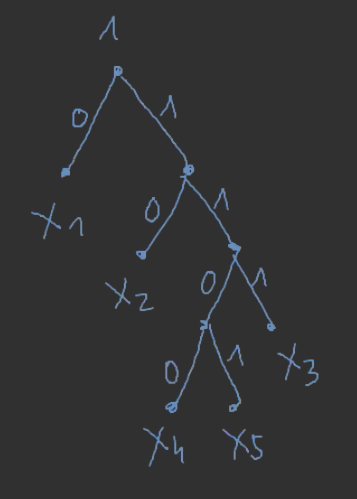
Czyli teraz możemy policzyć kody poszczególnych symboli:

3. Fakt o słowach kodowych Huffmana

  1. l1≤l2≤l3≤⋯≤lNl_1 \le l_2 \le l_3 \le \dots \le l_N (li=∣c(xi)∣l_i = |c(x_i)|)
  2. lN−1=lNl_{N-1} = l_N
  3. c(xN)c(x_N) oraz c(xN−1)c(x_{N-1}) różnią się tylko ostatnim bitem.

3.1. D-d

Punkty 2. oraz 3. są oczywiste.
(patrz przykład — pierwsze połączone wisienki)

  1. mniej oczywiste, zaraz zostanie wyjaśnione

4. Fakt o własnościach optymalnych kodów

  1. l1≤l2≤l3≤⋯≤lNl_1 \le l_2 \le l_3 \le \dots \le l_N
  2. lN−1=lNl_{N-1} = l_N

4.1. D-d

  1. Załóżmy, że li>ljl_i > l_j dla pewnego i<ji<j

    ∣c(xk)∣=lk|c(x_k)| = l_k.
    Robimy kodowanie c~\tilde{c}:

    lc~=∑k=1Npkl~k=∑k≠i,jpkl~k+pil~i+pjl~j=∑k≠j,ipklk+pilj+pjli<∑kpklkl_{\tilde{c}} = \sum_{k=1}^N p_k \tilde{l}_k = \sum_{k \neq i,j} p_k \tilde{l}_k + p_i \tilde{l}_i + p_j \tilde{l}_j = \sum_{k \neq j,i} p_k l_k + p_i l_j + p_j l_i < \sum_{k} p_k l_k,
    ponieważ
    pilj+pjli<pili+pjljp_i l_j + p_j l_i < p_i l_i + p_j l_j,
    pi(lj−li)<pj(lj−li)p_i (l_j - l_i) < p_j (l_j - l_i),
    pi>pjp_i > p_j
    (ostrość!)

    generalnie pi<pj  ⟹  li≤ljp_i < p_j \implies l_i \le l_j

  2. Jeśli lN≠lN−1l_N \neq l_{N-1}, to ln>lN−1l_n > l_{N-1} oraz lNl_N jedyna;
    tzn. {N}={i:li=lN}\{N\} = \{i: l_i = l_N\}

    c(xN)=ε1ε2…εlNc~(xN)=ε1ε2…εN−1c(x_N) = \varepsilon_1 \varepsilon_2 \dots \varepsilon_{l_N} \qquad \tilde{c}(x_N) = \varepsilon_1 \varepsilon_2 \dots \varepsilon_{N-1}
    c~(xk)=c(xk)\tilde{c}(x_k) = c(x_k) dla k<Nk < N
    L~<L\tilde{L} < L \quad sprzeczność

    Eureka: c~\tilde{c} jest prefiksowy!

5. Fakt#3

Istnieje kod optymalny cc (dla p1≥p2≥p3≥⋯≥pNp_1 \ge p_2 \ge p_3 \ge \dots \ge p_N) spełniający warunki:

  1. l1≤l2≤…lNl_1 \le l_2 \le \dots l_N
  2. lN−1=lNl_{N-1} = l_N
  3. c(xN)c(x_N) oraz c(xN−1)c(x_{N-1}) różnią się tylko ostatnim bitem.

5.1. D-d

Punkty 1. i 2. OK.

Aby zrobić 3., trzeba zmodyfikować kod optymalny, który mamy c′c'.

Liczby l1,…,lNl_1, \dots, l_N spełniają nierówność Kraft’a. Można zrobić kod prefiksowy spełniający dodatkowo punkt 3.

□\square

6. Twierdzenie o kodach Huffmana

— Kody Huffmana są optymalne!

6.1. D-d

(przez indukcję względem NN; N=1,2N=1,2 nie sprawia problemu)

Mamy {p1,p2,…,pN}\{p_1, p_2, \dots, p_N\} i robimy {q1,q2,…,qN−1}\{q_1, q_2, \dots, q_{N-1}\} gdzie qi=piq_i = p_i dla i≤N−2i \le N-2; qN−1=pN−1+pNq_{N-1} = p_{N-1} + p_N.

Niech:

LNL_N — średnia długość kodu Huffmana dla pp.

LN=∑i=1NpilI=∑i=1N−2pili+pN−1lN−1+pNlN⏟(pN−1+pN)lN=(∗)L_N = \sum_{i=1}^N p_i l_I = \sum_{i=1}^{N-2} p_i l_i + \underbrace{p_{N-1} l_{N-1} + p_N l_N}_{(p_{N-1} + p_N) l_N} = (*)
i niech:

Dalej: (∗)=∑i≠kqi′li′+qk−(lk′+1)=LN−1∗+pN−1+pN. (*) = \sum_{i\neq k}q_i' l_i' + q_k- (l_k' + 1) = \bold{L_{N-1}^* + p_{N-1} + p_N}.

Weźmy teraz optymalne kodowanie dla układu {p1,…,pN}\{p_1,\dots,p_N\}. Ma ono średnią długość LN∗L_N^*.

Wiemy, że optymalne kodowanie można zrobić tak, aby kody odpowiadające pN−1p_{N-1} i pNp_N były bliźniakami (czyli stanowiły jedną wisienkę).

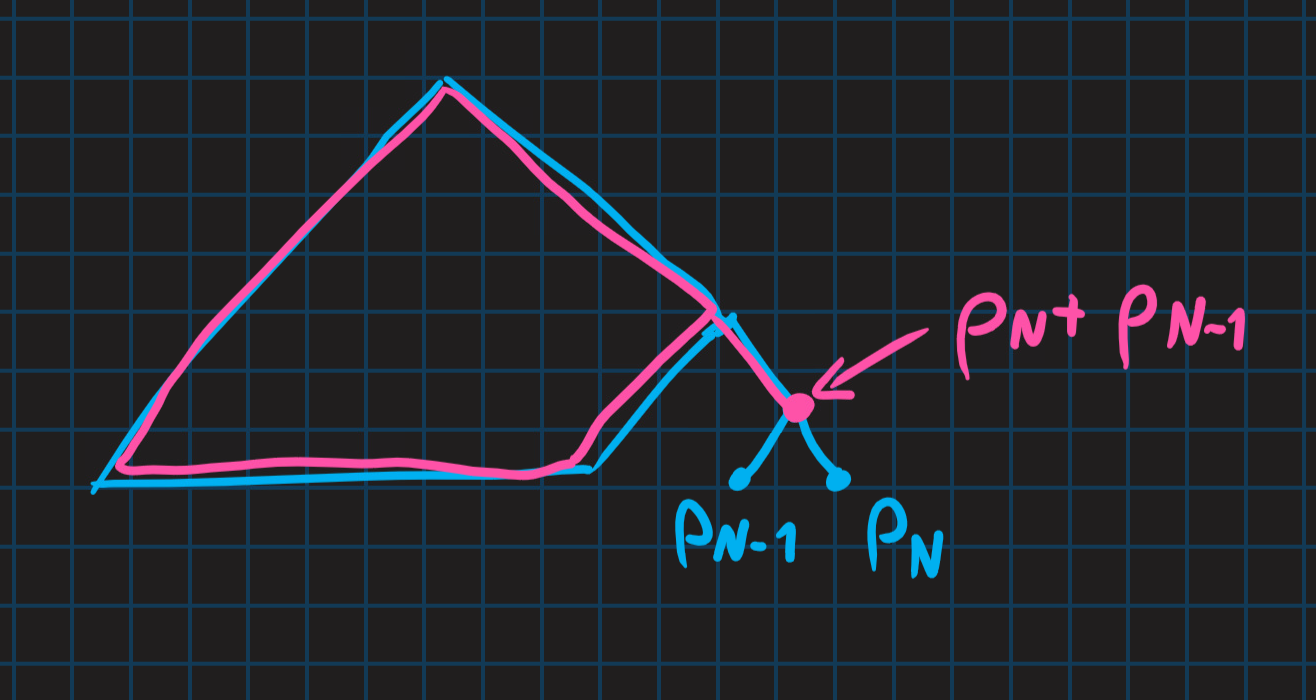
drzewa niebieskie i różowe: niebieskie to układ stary, różowe to układ z połączonymi wisienkami i w jeden

Optymalne „drzewa kodów” („∗*”) {p1,…,pN}\{p_1,\dots,p_N\} przerabiamy robiąc pewne drzewo kodów dla {p1,…,pN2,pN−1+pN}={q1,…,qN−1}\{p_1,\dots, p_{N_2}, p_{N-1} + p_N\} = \{q_1, \dots, q_{N-1}\}.

LN∗=∑i=1Nli∗piLN−1′=∑i=1N−1li′qi=∑i=1N−2li∗pi+(lN−1∗−1)⏟lN∗(pN−1+pN)=∑i=1Nli∗pi−pN−1−pN L_N^* = \sum_{i=1}^N l_i^* p_i \\[10pt] L_{N-1}' = \sum_{i=1}^{N-1} l_i' q_i = \sum_{i=1}^{N-2} l_i* p_i + \underbrace{(l_{N-1}^* - 1)}_{l_N^*} (p_{N-1} + p_N) =\\[5pt] \sum_{i=1}^N l_i^* p_i - p_{N-1} - p_N

Czyli LN−1′+pN−1+pN=LN∗. L_{N-1}' + p_{N-1} + p_N = L_N^*.

Wcześniej mieliśmy LN−1∗+pN−1+pN=LNL_{N-1}^* + p_{N-1} + p_N = L_N

Co jest dobre, ponieważ LN∗≤LNL_{N}^* \le L_N, bo LN∗L_{N}^* jest tym kodem idealnym. To samo się dzieje dla (N−1)(N-1): LN−1∗≤LN−1′L_{N-1}^* \le L_{N-1}'.

Zatem (z powyższych nierówności i równości), mamy LN=LN∗(oraz LN−1′=LN−1∗) L_N = L_N^* \quad (\text{oraz } L_{N-1}' = L_{N-1}^*)

□\square