Nierówność Kraft’a

• 1. Nierówność Kraft’a
  • 1.1. D-d
    • 1.1.1. Ćwiczenie
• 2. Fakt#1
  • 2.1. D-d
• 3. Fakt#2
  • 3.1. D-d

1. Nierówność Kraft’a

$\sum_{i=1}^{N} 2^{-l_i} \le 1$ (dla kodu prefiksowego)

1.1. D-d

Wizualizacja kodów prefiksowych (drzewo):

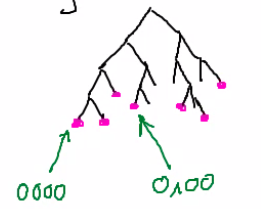
$l$ - maksymalna głębokość, czyli długość najdłuższego kodu

• ile liści na ostatnim poziomie „wyznacza” $i$-ta wisienka? (każda wisienka ma swoje pod-drzewka)

• kod $i$-tej wiśni jest długości $l_i$

• liczba liści to $2^{l-l_i}$

Zatem $$\sum_{i=1}^{N} 2^{l-l_i} \le 2^l \qquad\blacksquare$$

1.1.1. Ćwiczenie

Pokaż, że na odwrót.

2. Fakt#1

$\forall x>0 \qquad \ln(x) \le x-1$.

2.1. D-d

1. $f(x) = x-1-\ln(x) \qquad \boldsymbol| \text{ różniczkujemy}$
2. $f'(x) = 1 - \frac{1}{x}$
   1. $f'(x) < 0$ dla $x \in (0;1)$
   2. $f'(1) = 0$
   3. $f'(x) > 0$ dla $x > 1$
3. $f$ ma minimum w $1$.
4. $f(1) = 0$. $\blacksquare$

3. Fakt#2

$\log_2(x) = \log_2(e) \ln(x) \le (\log_2(e)) \cdot (x-1)$

3.1. D-d

(Twierdzenie Shannon’a)

$L - H = \sum_{i=1}^{N} p_i l_i + \sum_{i=1}^{N} p_i \log p_i = \sum_{i=1}^{N} p_i \log (2^{k_i} \cdot p_i)$

$H - L = \sum_{i=1}^{N} p_i \log\frac{1}{2^{l_i} \cdot p_i} \le \sum_{i=1}^{N} p_i \left( \frac{1}{2^{l_i} p_i} -1 \right) \log_2 (e) = \log_2(e) \left( \sum_{i=1}^{N} \frac{1}{2^{l_i}} - \sum_{i=1}^{N} p_i \right) \le \log_2(e) \left( 1 - 1 \right) = 0$
czyli sukces $\blacksquare$