1. Reprezentacja liczb w fl
notatka «Numeryczna reprezentacja liczb»
2. Oznaczenia działań
Niech
x = r d ( x ) x = rd(x) x = r d ( x ) y = r d ( y ) y = rd(y) y = r d ( y )
będą liczbami w arytmetyce fl , wówczas przez f l ( x ∗ y ) = f l ( x ⊛ y )
fl(x * y) = fl(x \circledast y)
f l ( x ∗ y ) = f l ( x ⊛ y ) x ∗ y x * y x ∗ y ∗ ∈ { + , − , / , ⋅ } * \in \{+, -, /, \cdot\} ∗ ∈ { + , − , / , ⋅ } fl .
3. Przykład
Mamy
β = 10 \beta = 10 β = 1 0 t = 5 t = 5 t = 5 x = r d ( x ) = 0.31426 ⋅ 1 0 3 x = rd(x) = 0.31426 \cdot 10^3 x = r d ( x ) = 0 . 3 1 4 2 6 ⋅ 1 0 3 y = r d ( y ) = 0.92577 ⋅ 1 0 5 y = rd(y) = 0.92577 \cdot 10^5 y = r d ( y ) = 0 . 9 2 5 7 7 ⋅ 1 0 5
Używamy akumulatora o podwójnej długości do pośrednich obliczeń.
x + y = po wyr o ˊ wnaniu cech 0.9289126000 ⋅ 1 0 5 → zaokrągl. f l ( x + y ) = 0.92891 ⋅ 1 0 5
x + y \overset{\text{po wyrównaniu cech}}{=} 0.9289126000 \cdot 10^5\\ \xrightarrow{\text{zaokrągl.}} fl(x + y) = 0.92891 \cdot 10^5
x + y = po wyr o ˊ wnaniu cech 0 . 9 2 8 9 1 2 6 0 0 0 ⋅ 1 0 5 zaokr ą gl. f l ( x + y ) = 0 . 9 2 8 9 1 ⋅ 1 0 5 x − y = po wyr o ˊ wnaniu cech − 0.9226274000 ⋅ 1 0 5 → zaokrągl. f l ( x − y ) = − 0.92263 ⋅ 1 0 5
x - y \overset{\text{po wyrównaniu cech}}{=} -0.9226274000 \cdot 10^5\\ \xrightarrow{\text{zaokrągl.}} fl(x-y) = -0.92263 \cdot 10^5
x − y = po wyr o ˊ wnaniu cech − 0 . 9 2 2 6 2 7 4 0 0 0 ⋅ 1 0 5 zaokr ą gl. f l ( x − y ) = − 0 . 9 2 2 6 3 ⋅ 1 0 5 x ⋅ y = 0.2909334802 ⋅ 1 0 8 → zaokrągl. f l ( x ⋅ y ) = 0.29093 ⋅ 1 0 8
x \cdot y = 0.2909334802 \cdot 10^8 \xrightarrow{\text{zaokrągl.}} fl(x \cdot y) = 0.29093 \cdot 10^8
x ⋅ y = 0 . 2 9 0 9 3 3 4 8 0 2 ⋅ 1 0 8 zaokr ą gl. f l ( x ⋅ y ) = 0 . 2 9 0 9 3 ⋅ 1 0 8 x y ≈ 0.3394579647 ⋅ 1 0 − 2 → zaokrągl. f l ( x y ) = 0.33946 ⋅ 1 0 − 2
\frac{x}{y} \approx 0.3394579647 \cdot 10^{-2} \xrightarrow{\text{zaokrągl.}} fl\left(\frac{x}{y}\right) = 0.33946 \cdot 10^{-2}
y x ≈ 0 . 3 3 9 4 5 7 9 6 4 7 ⋅ 1 0 − 2 zaokr ą gl. f l ( y x ) = 0 . 3 3 9 4 6 ⋅ 1 0 − 2
3.1. Błędy
Błędy względne:
∣ δ + ∣ ≈ 2.8 ⋅ 1 0 − 6 |\delta_+| \approx 2.8 \cdot 10^{-6} ∣ δ + ∣ ≈ 2 . 8 ⋅ 1 0 − 6 ∣ δ − ∣ ≈ 2.8 ⋅ 1 0 − 6 |\delta_-| \approx 2.8 \cdot 10^{-6} ∣ δ − ∣ ≈ 2 . 8 ⋅ 1 0 − 6 ∣ δ ⋅ ∣ ≈ 8.5 ⋅ 1 0 − 6 |\delta_{\cdot}| \approx 8.5 \cdot 10^{-6} ∣ δ ⋅ ∣ ≈ 8 . 5 ⋅ 1 0 − 6 ∣ δ / ∣ ≈ 6 ⋅ 1 0 − 6 |\delta_{/}| \approx 6 \cdot 10^{-6} ∣ δ / ∣ ≈ 6 ⋅ 1 0 − 6
Precyzja arytmetyki:ϵ = 5 ⋅ 1 0 − 5 \epsilon = 5 \cdot 10^{-5} ϵ = 5 ⋅ 1 0 − 5
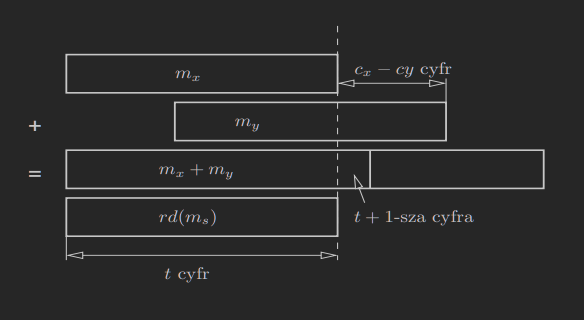
4. Przykład (dodawanie kiedy x ≫ y x \gg y x ≫ y
Niech
x = r d ( x ) = m x β c x x = rd(x) = m_x \beta^{c_x} x = r d ( x ) = m x β c x y = r d ( y ) = m y β c y y = rd(y) = m_y \beta^{c_y} y = r d ( y ) = m y β c y x ≥ y > 0 x \ge y > 0 x ≥ y > 0
Wówczas: x + y = m x β c x + m y β c y = ( m x + m y β − ( c x − c y ) ) β c x = m s β c x
x + y = m_x\beta^{c_x} + m_y \beta^{c_y} = (m_x + m_y\beta^{-(c_x - c_y)}) \beta^{c_x} = m_s \beta^{c_x}
x + y = m x β c x + m y β c y = ( m x + m y β − ( c x − c y ) ) β c x = m s β c x
Z powyższego rysunku wynika, że dla x ≫ y x \gg y x ≫ y f l ( x + y ) = x fl(x+y) = x f l ( x + y ) = x
5. Warunek na błędy
Arytmetyka fl powinna zapewnić równość f l ( x ∗ y ) = r d ( x ∗ y )
fl(x * y) = rd(x*y)
f l ( x ∗ y ) = r d ( x ∗ y ) ∗ ∈ { + , − , / , ⋅ } * \in \{+, -, /, \cdot\} ∗ ∈ { + , − , / , ⋅ } x ∗ y ∈ [ − M A X ; M A X ] x * y \in [-\mathrm{MAX};~ \mathrm{MAX}] x ∗ y ∈ [ − M A X ; M A X ]
Jeśli powyższe jest prawdziwe, to zachodzi równość f l ( x ∗ y ) = ( x ∗ y ) ( 1 + δ )
fl(x * y) = (x*y)(1 + \delta)
f l ( x ∗ y ) = ( x ∗ y ) ( 1 + δ ) ∣ δ ∣ ≤ ϵ |\delta| \le \epsilon ∣ δ ∣ ≤ ϵ ϵ = 0.5 β 1 − t \epsilon = 0.5\beta^{1-t} ϵ = 0 . 5 β 1 − t
6. Przykład (narastający błąd po 3 3 3
Obliczymy x ( y + z ) x(y + z) x ( y + z ) fl . (x = r d ( x ) x = rd(x) x = r d ( x ) y = r d ( y ) y = rd(y) y = r d ( y ) z = r d ( z ) z = rd(z) z = r d ( z )
f l ( x ( y + z ) ) = f l ( x ⋅ f l ( y + z ) ) = [ x ⋅ f l ( y + z ) ] ( 1 + δ 1 ) = [ x ( y + z ) ( 1 + δ 2 ) ] ( 1 + δ 1 ) = x ( y + z ) ( 1 + δ 2 + δ 1 + δ 2 δ 1 ) ≈ x ( y + z ) ( 1 + δ 2 + δ 1 ) = x ( y + z ) ( 1 + δ 3 ) fl(x(y+z)) = fl(x \cdot fl(y+z)) = [x \cdot fl(y+z)](1 + \delta_1) = [x(y+z)(1 + \delta_2)](1 + \delta_1) = x(y+z)(1 + \delta_2 + \delta_1 + \delta_2\delta_1) \approx x(y+z)(1+ \delta_2 + \delta_1) = x(y+z)(1+\delta_3) f l ( x ( y + z ) ) = f l ( x ⋅ f l ( y + z ) ) = [ x ⋅ f l ( y + z ) ] ( 1 + δ 1 ) = [ x ( y + z ) ( 1 + δ 2 ) ] ( 1 + δ 1 ) = x ( y + z ) ( 1 + δ 2 + δ 1 + δ 2 δ 1 ) ≈ x ( y + z ) ( 1 + δ 2 + δ 1 ) = x ( y + z ) ( 1 + δ 3 )
gdzie ∣ δ i ∣ ≤ ϵ , i = 1 , 2 |\delta_i| \le \epsilon,~ i = 1,2 ∣ δ i ∣ ≤ ϵ , i = 1 , 2 ∣ δ 3 ∣ ≤ 2 ϵ |\delta_3| \le 2\epsilon ∣ δ 3 ∣ ≤ 2 ϵ
7. Twierdzenie#1
Jeśli ∀ i = 1 , … , n ∣ δ i ∣ ≤ ϵ \forall i = 1,\dots,n \enspace |\delta_i| \le \epsilon ∀ i = 1 , … , n ∣ δ i ∣ ≤ ϵ ∏ i = 1 n ( 1 + δ i ) = 1 + E n \prod_{i=1}^n(1 + \delta_i) = 1 + E_n ∏ i = 1 n ( 1 + δ i ) = 1 + E n n ϵ < 2 n_\epsilon < 2 n ϵ < 2 ∣ E n ∣ < n ϵ 1 − 0.5 n ϵ ≈ n ϵ
|E_n| < \frac{n \epsilon}{1 - 0.5n\epsilon} \approx n\epsilon
∣ E n ∣ < 1 − 0 . 5 n ϵ n ϵ ≈ n ϵ
7.1. D-d
∣ E n ∣ = ∣ ∏ i = 1 n ( 1 + δ i ) − 1 ∣ ≤ ( 1 + ϵ ) n − 1 = 1 + ( n 1 ) ϵ + ( n 2 ) ϵ 2 + ( n 3 ) ϵ 3 + ⋯ + ( n n ) ϵ n − 1 = n ϵ + n ϵ ( n − 1 ) ϵ 2 ! + n ϵ ( n − 1 ) ϵ ( n − 2 ) ϵ 3 ! + ⋯ + n ϵ ( n − 1 ) ϵ ⋯ 1 ϵ n ! = n ϵ ( 1 + ( n − 1 ) ϵ 2 ! + ( n − 1 ) ϵ ( n − 2 ) ϵ 3 ! + ⋯ + ( n − 1 ) ϵ ⋯ 1 ϵ n ! ) q = n ϵ 2 < 1 ∣ E n ∣ < n ϵ ( 1 + q + q 2 + ⋯ + q n − 1 ) = n ϵ 1 − q n 1 − q < n ϵ 1 − 0.5 n ϵ ≈ n ϵ ■
\begin{aligned}
|E_n| &= \left|\prod_{i=1}^{n} (1 + \delta_i) - 1\right| \le (1 + \epsilon)^n - 1\\
&= 1 + \binom{n}{1}\epsilon + \binom{n}{2}\epsilon^2 + \binom{n}{3}\epsilon^3 + \dotsb + \binom{n}{n}\epsilon^n - 1\\
&= n\epsilon + \frac{n\epsilon(n-1)\epsilon}{2!} + \frac{n\epsilon(n-1)\epsilon(n-2)\epsilon}{3!} + \dotsb + \frac{n\epsilon(n-1)\epsilon\dotsb1\epsilon}{n!}\\
&= n\epsilon\left( 1 + \frac{(n-1) \epsilon}{2!} + \frac{(n-1)\epsilon(n-2)\epsilon}{3!} + \dotsb +\frac{(n-1) \epsilon \dotsb 1 \epsilon}{n!} \right)\\
&\qquad q = \frac{n\epsilon}{2} < 1\\
|E_n| &< n\epsilon(1 + q + q^2 + \dotsb + q^{n-1}) = n\epsilon \frac{1 - q^n}{1 - q} < \frac{n\epsilon}{1 - 0.5n\epsilon} \approx n\epsilon \quad \blacksquare
\end{aligned}
∣ E n ∣ ∣ E n ∣ = ∣ ∣ ∣ ∣ ∣ ∣ i = 1 ∏ n ( 1 + δ i ) − 1 ∣ ∣ ∣ ∣ ∣ ∣ ≤ ( 1 + ϵ ) n − 1 = 1 + ( 1 n ) ϵ + ( 2 n ) ϵ 2 + ( 3 n ) ϵ 3 + ⋯ + ( n n ) ϵ n − 1 = n ϵ + 2 ! n ϵ ( n − 1 ) ϵ + 3 ! n ϵ ( n − 1 ) ϵ ( n − 2 ) ϵ + ⋯ + n ! n ϵ ( n − 1 ) ϵ ⋯ 1 ϵ = n ϵ ( 1 + 2 ! ( n − 1 ) ϵ + 3 ! ( n − 1 ) ϵ ( n − 2 ) ϵ + ⋯ + n ! ( n − 1 ) ϵ ⋯ 1 ϵ ) q = 2 n ϵ < 1 < n ϵ ( 1 + q + q 2 + ⋯ + q n − 1 ) = n ϵ 1 − q 1 − q n < 1 − 0 . 5 n ϵ n ϵ ≈ n ϵ ■
8. Przykład (narastający błąd po n n n
Mamy:
x i > 0 x_i > 0 x i > 0 i = 0 , … , n i = 0,\dots, n i = 0 , … , n
Obliczyć:
S = ∑ i = 0 n x i S = \sum_{i=0}^n x_i S = ∑ i = 0 n x i
Algorytm:
S 0 = x 0 S_0 = x_0 S 0 = x 0 for i : = 1 i := 1 i : = 1 to n n n do:
S i : = S i − 1 + x i S_i := S_{i-1} + x_i S i : = S i − 1 + x i end for
f l ( S ) = f l ( … f l ( f l ( f l ( x 0 + x 1 ) + x 2 ) + x 3 ) + ⋯ + x n ) = ( … ( ( ( x 0 + x 1 ) ( 1 + δ 1 ) + x 2 ) ( 1 + δ 2 ) + + x 3 ) ( 1 + δ 3 ) + ⋯ + x n ) ( 1 + δ n ) = x 0 ∏ i = 1 n ( 1 + δ i ) + x 1 ∏ i = 1 n ( 1 + δ i ) + + x 2 ∏ i = 2 n ( 1 + δ i ) + x 3 ∏ i = 3 n ( 1 + δ i ) + ⋯ + x n ( 1 + δ n )
\begin{aligned}
fl(S) &= fl(\dots fl(fl(fl(x_0 + x_1) + x_2) + x_3) + \dotsb + x_n)\\
&= (\dots (((x_0 + x_1)(1 + \delta_1) + x_2)(1 + \delta_2) +\\
&+ x_3)(1 + \delta_3) + \dotsb + x_n)(1 + \delta_n)\\
&= x_0 \prod_{i=1}^{n}(1 + \delta_i) + x_1\prod_{i=1}^{n}(1 + \delta_i)+\\
&+ x_2\prod_{i=2}^{n}(1+\delta_i) + x_3\prod_{i=3}^{n}(1+\delta_i) + \dotsb + x_n (1+\delta_n)
\end{aligned}
f l ( S ) = f l ( … f l ( f l ( f l ( x 0 + x 1 ) + x 2 ) + x 3 ) + ⋯ + x n ) = ( … ( ( ( x 0 + x 1 ) ( 1 + δ 1 ) + x 2 ) ( 1 + δ 2 ) + + x 3 ) ( 1 + δ 3 ) + ⋯ + x n ) ( 1 + δ n ) = x 0 i = 1 ∏ n ( 1 + δ i ) + x 1 i = 1 ∏ n ( 1 + δ i ) + + x 2 i = 2 ∏ n ( 1 + δ i ) + x 3 i = 3 ∏ n ( 1 + δ i ) + ⋯ + x n ( 1 + δ n ) ∣ δ i ∣ ≤ ϵ , i = 1 , … , n |\delta_i| \le \epsilon,~ i = 1,\dots, n ∣ δ i ∣ ≤ ϵ , i = 1 , … , n
Podstawmy ∏ i = k n ( 1 + δ i ) = 1 + E k \prod_{i=k}^{n}(1 + \delta_i) = 1+E_k ∏ i = k n ( 1 + δ i ) = 1 + E k f l ( S ) = x 0 + x 0 E 1 + x 1 + x 1 E 1 + x 2 + x 2 E 2 + x 3 + x 3 E 3 + ⋯ + x n + x n E n = S + x 0 E 1 + x 1 E 1 + x 2 E 2 + x 3 E 3 + ⋯ + x n E n ≤ S + ( x 0 + x 1 + x 2 + x 3 + ⋯ + x n ) max 1 ≤ k ≤ n E k = S ( 1 + E 1 )
\begin{aligned}
fl(S) &= x_0 + x_0E_1 + x_1 + x_1E_1 + x_2 + x_2E_2 + x_3 + x_3E_3 + \dotsb + x_n + x_nE_n\\
&= S + x_0E_1 + x_1E_1 + x_2E_2 + x_3E_3 + \dotsb + x_nE_n\\
&\le S + (x_0 + x_1 + x_2 + x_3 + \dotsb + x_n)\max_{1 \le k \le n} E_k = S(1 + E_1)
\end{aligned}
f l ( S ) = x 0 + x 0 E 1 + x 1 + x 1 E 1 + x 2 + x 2 E 2 + x 3 + x 3 E 3 + ⋯ + x n + x n E n = S + x 0 E 1 + x 1 E 1 + x 2 E 2 + x 3 E 3 + ⋯ + x n E n ≤ S + ( x 0 + x 1 + x 2 + x 3 + ⋯ + x n ) 1 ≤ k ≤ n max E k = S ( 1 + E 1 ) ∣ E 1 ∣ < n ϵ |E_1| < n\epsilon ∣ E 1 ∣ < n ϵ «Twierdzenie#1» .
9. Redukcja cyfr znaczących
Przeanalizujmy zjawisko redukcji cyfr znaczących:
r d ( x ) = x ( 1 + δ x ) rd(x) = x(1 + \delta_x) r d ( x ) = x ( 1 + δ x ) r d ( y ) = y ( 1 + δ y ) rd(y) = y(1 + \delta_y) r d ( y ) = y ( 1 + δ y )
∣ x − y − [ r d ( x ) − r d ( y ) ] ∣ ∣ x − y ∣ = ∣ δ x x − δ y y ∣ ∣ x − y ∣ ≤ ϵ ∣ x ∣ + ∣ y ∣ ∣ x − y ∣
\frac{|x - y - [rd(x) - rd(y)]|}{|x - y|} = \frac{|\delta_x x - \delta_y y|}{|x - y|} \le \epsilon\frac{|x| + |y|}{|x - y|}
∣ x − y ∣ ∣ x − y − [ r d ( x ) − r d ( y ) ] ∣ = ∣ x − y ∣ ∣ δ x x − δ y y ∣ ≤ ϵ ∣ x − y ∣ ∣ x ∣ + ∣ y ∣
Z powyższego oszacowania wynika, że niedokładność danych może przenieść się na wynik z wielkim mnożnikiem ∣ x ∣ + ∣ y ∣ ∣ x − y ∣ \frac{|x| + |y|}{|x - y|} ∣ x − y ∣ ∣ x ∣ + ∣ y ∣
9.1. Przykład
Niech
x = 0.3721478693 x = 0.3721478693 x = 0 . 3 7 2 1 4 7 8 6 9 3 y = 0.3720230572 y = 0.3720230572 y = 0 . 3 7 2 0 2 3 0 5 7 2
(x ≈ y x \approx y x ≈ y
Różnica dokładna to x − y = 0.0001248121 x - y = 0.0001248121 x − y = 0 . 0 0 0 1 2 4 8 1 2 1
Policzymy x − y x - y x − y fl .
t = 5 t = 5 t = 5 r d ( x ) = 0.37215 rd(x) = 0.37215 r d ( x ) = 0 . 3 7 2 1 5 r d ( y ) = 0.37202 rd(y) = 0.37202 r d ( y ) = 0 . 3 7 2 0 2 f l ( r d ( x ) − r d ( y ) ) = 0.00013 fl(rd(x) - rd(y)) = 0.00013 f l ( r d ( x ) − r d ( y ) ) = 0 . 0 0 0 1 3
Zauważmy, że tutaj mamy f l ( r d ( x ) − r d ( y ) ) = r d ( x ) − r d ( y ) fl(rd(x) - rd(y)) = rd(x) - rd(y) f l ( r d ( x ) − r d ( y ) ) = r d ( x ) − r d ( y )
∣ δ ∣ = ∣ x − y − [ r d ( x ) − r d ( y ) ] ∣ ∣ x − y ∣ = ∣ 0.0001248121 − 0.00013 ∣ 0.0001248121 ∣ ≈ 4.16 ⋅ 1 0 − 2 |\delta| = \frac{|x - y - [rd(x) - rd(y)]|}{|x - y|} = \frac{|0.0001248121 - 0.00013}{|0.0001248121|} \approx 4.16 \cdot 10^{-2} ∣ δ ∣ = ∣ x − y ∣ ∣ x − y − [ r d ( x ) − r d ( y ) ] ∣ = ∣ 0 . 0 0 0 1 2 4 8 1 2 1 ∣ ∣ 0 . 0 0 0 1 2 4 8 1 2 1 − 0 . 0 0 0 1 3 ≈ 4 . 1 6 ⋅ 1 0 − 2
Precyzja arytmetyki ϵ = 5 ⋅ 1 0 − 5 \epsilon = 5 \cdot 10^{-5} ϵ = 5 ⋅ 1 0 − 5
9.2. Przykład
Gdy liczymy wartość wyrażenia x 2 + 1 − 1 \sqrt{x^2 + 1} - 1 x 2 + 1 − 1 ∣ x ∣ \bold{|x|} ∣ x ∣ jest mała .
Przekształćmy x 2 + 1 − 1 \sqrt{x^2 + 1} - 1 x 2 + 1 − 1 y = ( x 2 + 1 − 1 ) x 2 + 1 + 1 x 2 + 1 + 1 = x 2 x 2 + 1 + 1 .
y = (\sqrt{x^2 + 1 } - 1) \frac{\sqrt{x^2 + 1} + 1}{\sqrt{x^2 + 1} + 1} = \frac{x^2}{\sqrt{x^2 + 1} + 1}.
y = ( x 2 + 1 − 1 ) x 2 + 1 + 1 x 2 + 1 + 1 = x 2 + 1 + 1 x 2 .
10. Twierdzenie#2
Ile cyfr znaczących tracimy przy odejmowaniu x − y x - y x − y x ≈ y x \approx y x ≈ y
Jeśli x x x y y y fl takimi, że x > y x > y x > y 2 − q ≤ 1 − y x ≤ 2 − p 2^{-q} \le 1 - \frac{y}{x} \le 2^{-p} 2 − q ≤ 1 − x y ≤ 2 − p p p p q q q
10.1. D-d
Niech x x x y y y fl , czyli x = m x 2 c x , y = m y 2 c y , x = m_x 2^{c_x},~ y = m_y 2^{c_y}, x = m x 2 c x , y = m y 2 c y , m x , m y ∈ [ 1 2 ; 1 ) m_x, m_y \in \left[\frac{1}{2};~ 1\right) m x , m y ∈ [ 2 1 ; 1 )
Ponieważ x > y x > y x > y r = x − y r = x-y r = x − y r = m x 2 c x − m y 2 c y = ( m x − m y 2 c y − c x ) ⋅ 2 c x = m r 2 c x
r = m_x 2^{c_x} - m_y 2^{c_y} = (m_x - m_y 2^{c_y - c_x})\cdot 2^{c_x} = m_r 2^{c_x}
r = m x 2 c x − m y 2 c y = ( m x − m y 2 c y − c x ) ⋅ 2 c x = m r 2 c x
Mantysa m r m_r m r m r = ( m x − m y 2 c y − c x ) = m x ( 1 − m y 2 c y m x 2 c x ) = m x ( 1 − y x ) < 2 − p .
m_r = (m_x - m_y 2^{c_y - c_x}) = m_x \left( 1 - \frac{m_y 2^{c_y}}{m_x 2^{c_x}} \right) = m_x\left( 1 - \frac{y}{x} \right) < 2^{-p}.
m r = ( m x − m y 2 c y − c x ) = m x ( 1 − m x 2 c x m y 2 c y ) = m x ( 1 − x y ) < 2 − p .
Aby znormalizować reprezentację x − y x - y x − y fl , musimy przesunąć mantysę m r m_r m r p p p p p p
Rozumowanie dla drugiej części jest podobne.