Własności języków bezkontekstowych

• 1. Lemat o pompowaniu dla języków bezkontekstowych
  • 1.1. D-d
  • 1.2. Przykład
  • 1.3. Przykład
• 2. Lemat Ogdena — silniejsza wersja lematu o pompowaniu
  • 2.1. D-d
  • 2.2. Przykład
• 3. Twierdzenie o zamkniętności operacji na j. bezkontekstowych
  • 3.1. D-d
• Twierdzenie o nie-zamkniętności operacji przecięcia na j. bezkontekstowych
  • D-d

1. Lemat o pompowaniu dla języków bezkontekstowych

Niech $L$ będzie dowolnym językiem bezkontekstowym. Wówczas istnieje stała pompowania $n$, zależna tylko od $L$, taka, że jeśli słowo $z$ należy do języka $L$ oraz $|z| \ge n$, to $z = uvwxy$, oraz

• $|vx| \ge 1$
• $|vwx| \le n$
• dla każdego $i \ge 0$ mamy $uv^iwx^iy \in L$

(ten lemat rozszerza ten poprzedni lemat o pompowaniu dodając jeszcze pole $x$)

1.1. D-d

Mamy gramatykę $G(L)$ w postaci normalnej Chomsky’ego (czyli mamy produkcje typu $A \to BC$ lub $A \to a$; drzewo wyprowadzenia jest binarne patrząc na węzły wewnętrzne).

Niech ta nasza gramatyka $G = (N,T,P,S)$ gdzie $|N| = k$.

Ustalmy $n = 2^k$ (stałą pompowania).
Bierzemy $z \in L$, $z = z_1,\dots,z_n$ (składa się z $n$ symboli).

Drzewo wyprowadzenia:

Bierzemy najdłuższą ścieżkę, która jest długości co najmniej długości $\lg n = k$. Ścieżka zawiera co najmniej $k+1$ węzłów wewnętrznych, ale mamy tylko $k$ nieterminali — czyli (pigeonhole principle) musimy mieć gdzieś powtórkę (oznaczmy przez $A$). Patrząc od dołu zaznaczamy poddrzewa, których korzeniami są te dwie instancje $A$:

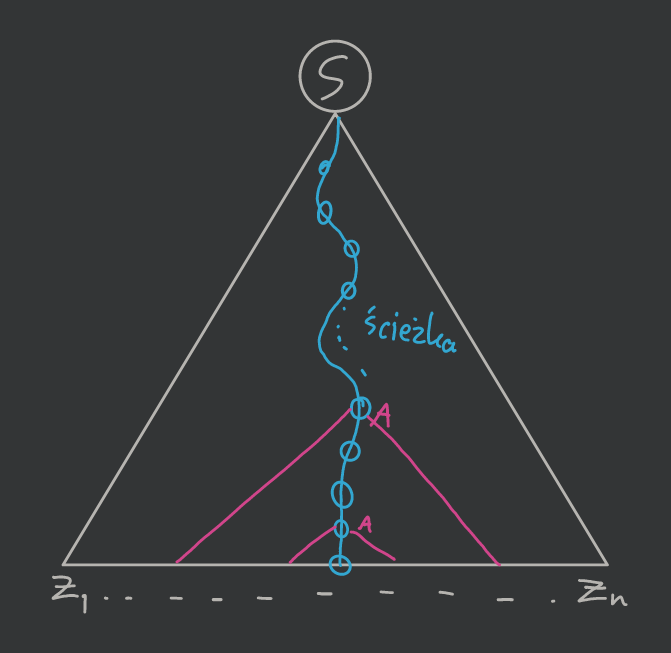
Stosujemy podział słowa $z = uvwxy$:

I możemy je teraz „pompować”:

1. $uv^0wx^0y$
   
2. $yv^2wx^2y$
   

Dlatego lemat jest spełniony.

Chociaż jeszcze należy pokazać, że:

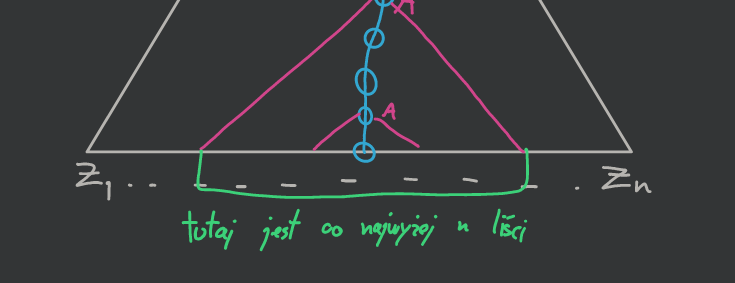
Wynika to z tego, że szukaliśmy pierwszych powtarzających się symboli od dołu, stąd poddrzewo (czerwone, większe) nie może być wyższe niż $k$. Co daje nam liczbę liści $\le 2^k$.

1.2. Przykład

Mamy język $L = \left\{ a^i b^i c^i: i \ge 1 \right\}$.

Używamy lematu w celu udowodnienia, że język $L$ nie jest bezkontekstowy.

Weźmy $n$ (stałą pompowania) i słowo $z = a^n b^n c^n$.

1. Zgodnie z lematem możemy pompować w obrębie jednego bloku znaków ($a$ lub $b$ lub $c$) ale wtedy zmienia się liczba tych znaków, a nie zmienia się liczba pozostałych, czyli wychodzimy z języka.
2. Możemy pompować też znaki z dwóch sąsiednich bloków ($a$ i $b$ lub $b$ i $c$) utrzymując ich równoliczność, ale wtedy zostaje problem z trzecim blokiem i także wypadamy z języka.
3. Innych możliwości nie ma więc $L$ nie jest bezkontekstowy.

1.3. Przykład

Mamy język $L = \left\{ a^i b^j c^k: i \neq j \land j \neq k \right\}$.

Bierzemy słowo $a^n b^{n+1} c^{n+2}$. Ale pompując w sposób $a^n b^{n-1} (b^2)^i (c^2)^i c^n$ dostajemy słowa należące do języka.

Musimy wzmocnić ten lemat.

2. Lemat Ogdena — silniejsza wersja lematu o pompowaniu

Niech $L$ będzie językiem bezkontekstowym. Wówczas istnieje stała pompowania $n$ taka, że jeśli w słowie $z \in L$ oznaczymy co najmniej $n$ liter to możemy słowo $z$ zapisać jako $uvwxy$ i

• $v$ oraz $x$ mają łącznie co najmniej jedną oznaczoną literę
• $vwx$ ma co najwyżej $n$ oznaczonych liter
• dla każdego $i \ge 0$ mamy $u v^i w x^i y \in L$.

2.1. D-d

Weźmy $m > n$, gdzie $n = 2^{|N|}$ i nasze słowo $z = z_1 z_2 \dots z_n \dots z_m$. Oznaczamy co najmniej $n$ liter.

Znowu, tak jak wcześniej, budujemy drzewo wyprowadzenia i najdłuższą ścieżkę czyli od korzenia do liścia, tylko tym razem w następujący sposób:
jeśli jestem w danym wierzchołku to idę do poddrzewa, które ma „więcej” symboli oznaczonych w liściach.

Wyznaczona ścieżka ma co najmniej długość $\lg n = k$. Co więcej jeśli zignorujemy wierzchołki, w których tylko jedno poddrzewo miało wierzchołki oznaczone to dalej mamy długość $k$.

Znowu, tak samo jak w poprzednim dowodzie mamy powtórki gdzieś wierzchołka $A$.

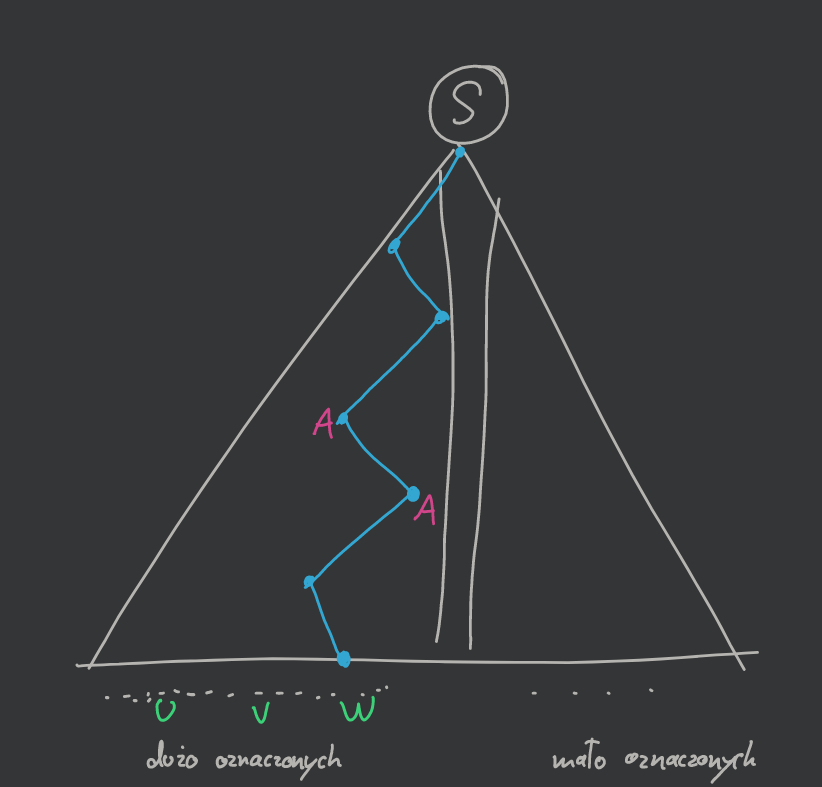
Więc analogicznie bierzemy poddrzewa:

Analiza podobna jak w poprzednim dowodzie, ale liczymy tylko symbole oznaczone.

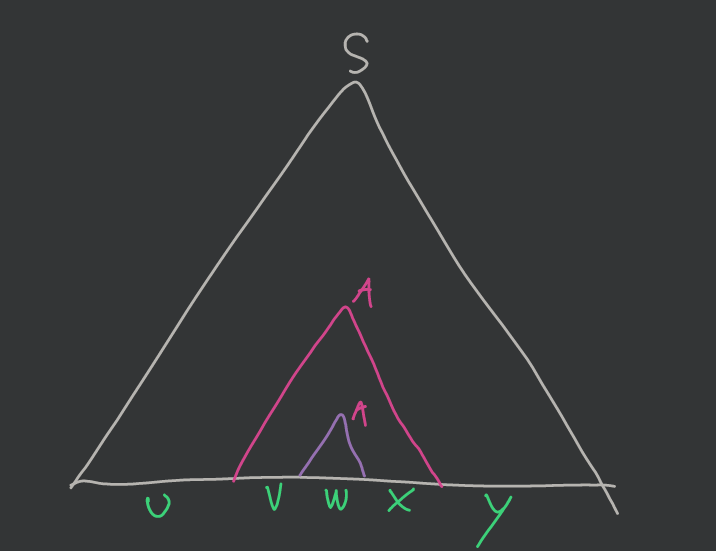
W obu połówkach były symbole oznaczone, to $v$ i $x$ muszą mieć jakiś symbol oznaczony.

3. Analogicznie, skoro liczyliśmy od dołu to wysokość (różowego) poddrzewa jest nie większa niż $k$ wierzchołków dzielących symbole oznaczone, stąd $vwx$ nie ma więcej niż $2^k = n$ symboli.

2.2. Przykład

Kontynuacja przykładu

Mamy język $L = \left\{ a^i b^j c^k: i \neq j \land j \neq k \right\}$.

Mamy $m > n$, gdzie $n$ to stała pompowania.

Bierzemy słowo $z = a^{m + m!} b^m c^{m + m!}$ — powinniśmy pompować najrzadziej występujący symbol.

Oznaczamy wszystkie litery $b$.

Zgodnie z lematem możemy:

1. Pompować tylko litery $b$; jeśli pompujemy $k$ liter to dla $i = \frac{m!}{k} + 1$ czyli mamy równość $b$ i $a$.
2. Pompować tylko $a$ i $b$ ($b$ i $c$) — znowu wypadamy z języka bo $b$ zrównają się z $c$ ($b$ z $a$).
3. Czy możemy równocześnie pompować $a$, $b$ i $c$? — nie, bo to by nam już nie zapewniło wypadnięcia z języka.

3. Twierdzenie o zamkniętności operacji na j. bezkontekstowych

Języki bezkontekstowe są zamknięte na sumę, złożenie i domknięcie Kleene’ego.

3.1. D-d

Niech

• $G_1 = (N_1, T_1, S_1, P_1)$
• $G_2 = (N_2, T_2, S_2, P_2)$

przy czym $N_1 \cap N_2 = \emptyset$ i $S \notin N_1 \cup N_2$.

1. $G_3 = \left(\{S\} \cup N_1 \cup N_2, T_1 \cup T_2, S, P_1 \cup P_2 \cup \{S \to S_1|S_2\} \right)$ i $L(G_3) = L(G_1) \cup L(G_2)$
2. $G_4 = \left( \{S\} \cup N_1 \cup N_2, T_1 \cup T_2, S, P_1 \cup P_2 \cup \{S \to S_1S_2\} \right)$ i $L(G_4) = L(G_1)L(G_2)$
3. $G_5 = \left( \{S\} \cup N_1, T_1, S, P_1 \cup \{S \to S_1 S | \epsilon\} \right)$ i $L(G_5) = L(G_1)^*$

Twierdzenie o nie-zamkniętności operacji przecięcia na j. bezkontekstowych

Języki bezkontekstowe nie są zamknięte na przecięcie.

D-d

Niech

• $A = \left\{ a^i b^i c^i \right\}$
• $B = \left\{ a^i b^i c^j \right\}$ jest j. bezkontekstowym bo $S \to AB, \enspace A \to \epsilon|aAb \enspace B \to \epsilon|cB$
• $C = \left\{ a^j b^i c^i \right\}$ (podobnie jak $B$)

Wówczas zauważmy, że
$A = B \cap C$ nie jest bezkontekstowy (przykład).