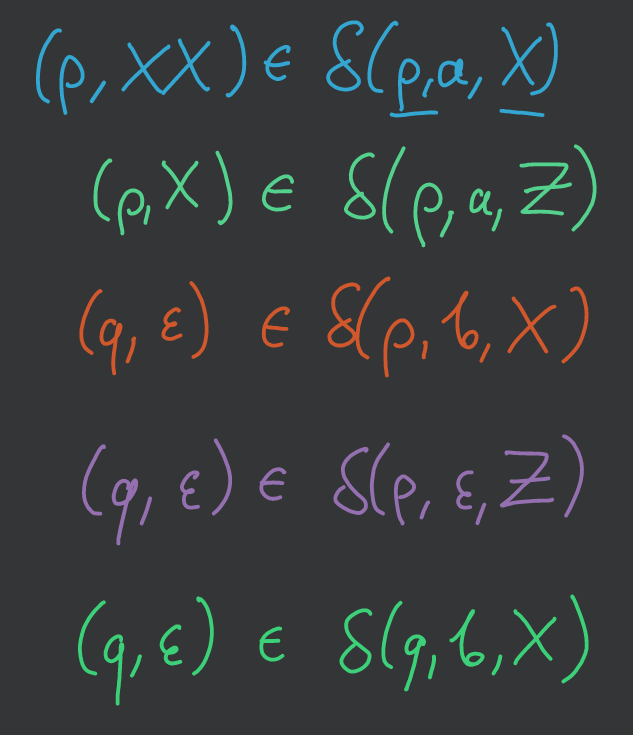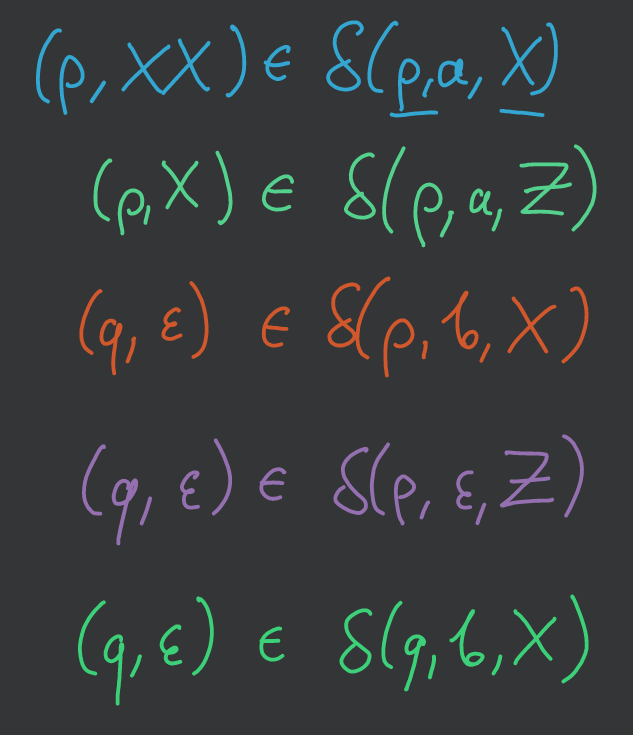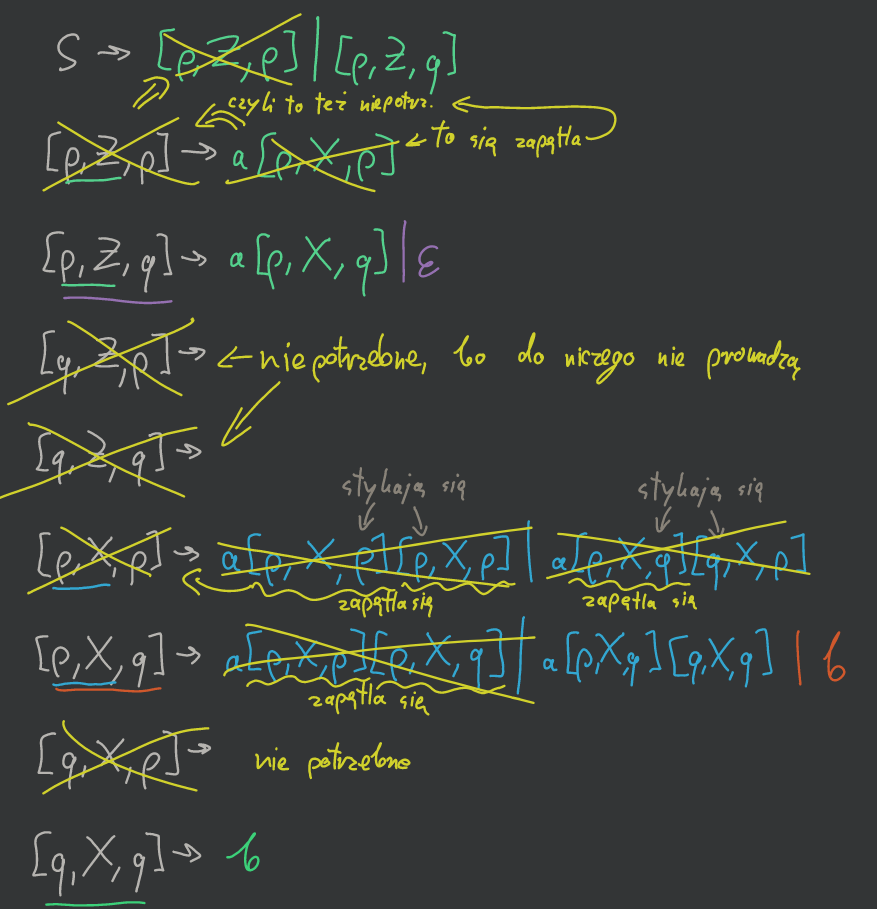Automat ze stosem (PDA)

• 1. DEF: PDA
  • 1.1. DEF: Opis chwilowy automatu
  • 1.2. DEF: Relacja przejścia w jednym kroku $\vdash_M$
  • 1.3. Sposoby akceptowania słów języka
• 2. Przykład
• 3. Przykład
• 4. Deterministyczny PDA
• 5. Twierdzenie: język bezkontekstowy $\implies$ PDA
  • 5.1. D-d
  • 5.2. Przykład
• 6. Twierdzenie: PDA $\implies$ język bezkontekstowy
  • 6.1. D-d
  • 6.2. Przykład

1. DEF: PDA

Automat z dodatkową pamięcią w postaci stosu (widać tylko ostatnio włożony symbol).

Automatem ze stosem nazywamy $M = (Q,\Sigma, \Gamma, \delta, q_0, Z_0, F)$, gdzie

• $Q$ — skończony zbiór stanów
• $\Sigma$ — alfabet wejściowy
• $\Gamma$ — alfabet stosowy
• $q_0 \in Q$ — stan początkowy
• $Z_0 \in \Gamma$ — symbol początkowy na stosie
• $F \in Q$ — zbiór stanów akceptujących (jeśli $F = \emptyset$ to akceptujemy przez pusty stos)
• $\delta$ funkcja przejścia postaci: $\delta: Q\times\left( \Sigma \cup \{\epsilon\} \right) \times \Gamma \to 2^{Q \times \Gamma^*}$

1.1. DEF: Opis chwilowy automatu

— to trójka $(q, \alpha, \gamma)$, gdzie

• $q \in Q$ — stan automatu
• $\alpha \in \Sigma^*$ — nieprzeczytane jeszcze wejście
• $\gamma \in \Gamma^*$ — zawartość stosu (szczyt stosu z lewej strony)

1.2. DEF: Relacja przejścia w jednym kroku $\vdash_M$

$\vdash^*$ — zwrotne i przechodnie domknięcie $\vdash$,
$\vdash^i$ — $i$-krotne złożenie $\vdash$.

• $(q, a\alpha, Z_\gamma) \vdash_M (p_i, \alpha, \gamma_i\gamma)$ jeśli istnieje przejście $\delta(q, a, Z) = \left\{ (p_1,\gamma_1), \dots, (p_m, \gamma_m) \right\}$ i wybraliśmy $i$-tą możliwość.
• $(q, \alpha, Z_\gamma) \vdash_M (p_i, \alpha, \gamma_i\gamma)$ jeśli istnieje przejście $\delta(q, \epsilon, Z) = \left\{ (p_1, \gamma_1), \dots, (p_m, \gamma_m) \right\}$ i wybraliśmy $i$-tą możliwość.

1.3. Sposoby akceptowania słów języka

1. Język Akceptowany przez PDA $M$ przy pustym stosie ($F = \emptyset$) to $$N(M) = \left\{ w \in \Sigma^*: \exists p\in Q \enspace (q_0, w, Z_0) \vdash^* (p, \epsilon, \epsilon) \right\}$$

2. Język akceptowany przez PDA $M$ przez stan końcowy to $$L(M) = \left\{ w \in \Sigma^*: \exists p\in F \enspace \exists \gamma\in \Gamma^* \enspace (q, w, Z_0) \vdash^* (p, \epsilon, \gamma) \right\}$$

Oba sposoby akceptowania są równoważne.

2. Przykład

Palindrom z gramatyką $S \to 0S0|1S1|\#$

1. Automat startuje z pustym stosem i w stanie $q_1$.
2. Jeżeli jesteśmy w stanie $q_1$ i na wejściu widzimy $a \in \{0,1\}$ to wstawiamy $a$ na stos, pozostajemy w stanie $q_1$ i idziemy do następnego symbolu wejściowego.
3. Jeżeli jesteśmy w stanie $q_1$ i na wejściu widzimy $\#$ to przechodzimy do stanu $q_2$ i idziemy do następnego symbolu wejściowego.
4. Jeżeli jesteśmy w stanie $q_2$ i na wejściu widzimy $a \in \{0,1\}$ i na stosie jest także $a$ to pozostajemy w stanie $q_2$, ściągamy $a$ ze stosu i idziemy do następnego symbolu wejściowego.
5. Jeżeli jesteśmy w stanie $q_2$, skończyliśmy czytać wejście i stos jest pusty, to akceptujemy słowo wejściowe.
6. W każdym innym przypadku odrzucamy słowo wejściowe.

3. Przykład

Mamy maszynę $M = \left( \{q_1,q_2\}, \{0,1\}, \{A,B,Z\}, \delta, q_1, Z, \emptyset \right)$

Przykładowo dla $0110$:
$(q_1, 0110, Z) \vdash (q_1, 110, A) \vdash (q_1, 10, BA) \vdash (q_2, 10, BA) \vdash (q_2, 0, A) \vdash (q_2, \epsilon, \epsilon)$

Za to $110$ nie należy do języka:

1. $(q_1, 110, Z) \vdash (q_1, 10, B) \vdash (q_1, 0, BB) \vdash (q_1, \epsilon, ABB) \vdash (q_2, \epsilon, ABB) \vdash ?$
2. $(q_1, 110, Z) \vdash (q_1, 10, B) \vdash (q_1, 0, BB) \vdash (q_2, 0, BB) \vdash ?$
3. $(q_1, 110, Z) \vdash (q_1, 10, B) \vdash (q_2, 10, B) \vdash (q_2, 0, \epsilon) \vdash ?$
4. $(q_1, 110, Z) \vdash (q_2, 100, \epsilon) \vdash ?$

Oczywiście mamy język $N(M) = \left\{ ww^R: w \in \{0,1\}^* \right\}$.

4. Deterministyczny PDA

PDA może być deterministyczny, jeśli w każdym przypadku możemy wykonać co najwyżej jedno przejście (czyli może też być zero przejść w przeciwieństwie do zwykłego DFA):

1. $\forall q \in Q \enspace \forall Z \in \Gamma \enspace \delta(q, \epsilon, Z) \neq \emptyset \implies \forall a \in \Sigma \enspace \delta(q,a,Z) = \emptyset$
2. $\forall q \in Q \enspace \forall a \in \Sigma \cup \{\epsilon\} \enspace \forall Z \in \Gamma \enspace \left\lvert \delta(q, a, Z) \right\rvert \le 1$

Niestety takie DPDA są słabsze od PDA.
Np. język z przykładu nie jest rozpoznawalny przez żaden DPDA.

5. Twierdzenie: język bezkontekstowy $\implies$ PDA

Jeśli $L$ jest językiem bezkontekstowym to istnieje PDA $M$ taki, że $L = N(M)$.

5.1. D-d

Załóżmy, że $L$ nie zawiera $\epsilon$ i jest zdefiniowany przez gramatykę bezkontekstową w postaci Greibach $G = (N, T, P, S)$. Definiujemy PDA $M$ następująco:

• $M = \left( \{q\}, T, N, \delta, q, S, \emptyset \right)$
• $\delta(q, a, A) = \left\{ (q, \gamma): (A \to a\gamma) \in P \right\}$.

$M$ symuluje wprowadzenie lewostronne gramatyki $G$. Ponieważ $G$ jest typu Greibach każdy kolejny napis w wyprowadzeniu lewostronnym ma formę $x\alpha$, gdzie $x \in T^*$ oraz $\alpha \in N^*$. Maszyna $M$ przechowuje $\alpha$ na stosie po przeczytaniu przedrostka $x$.

Teraz d-d indukcyjny po długości wyprowadzenia (liczby kroków), że $$S \underset{G}{\Rightarrow}^* \iff (q, x, S) \underset{M}{\vDash}^* (q, \epsilon, \epsilon)$$

5.2. Przykład

$G = \left( \{A,B\}, \{a,b\}, \{A \to aAB|aB, B \to b\}, A \right)$

A więc $M = \left( \{q\}, \{a,b\}, \{A,B\}, \delta, q, A, \emptyset \right)$

Czyli na przykład mamy:
$A \Rightarrow aAB \Rightarrow aaBB \Rightarrow aabB \Rightarrow aabb$.

I właśnie teraz równoważnie:
$(q, aabb, A) \vdash (q, abb, AB) \vdash (q, bb, BB), \vdash (q, b, B) \vdash (q, \epsilon, \epsilon)$.

6. Twierdzenie: PDA $\implies$ język bezkontekstowy

Jeśli $L = N(M)$ dla PDA $M$ to $L$ jest językiem bezkontekstowym.

6.1. D-d

Weźmy PDA $M = (Q, \Sigma, \Gamma, \delta, q_0, Z_0, \emptyset)$. Konstruujemy gramatykę bezkontekstową $G = (N, \Sigma, P, S)$, gdzie

• $N$ — zbiór obiektów postaci $[q, A, p]$ ($p, q \in Q, A \in \Gamma$) oraz nowy symbol $S$
• $P$ — zbiór produkcji postaci:
  • $S \to [q_0, Z_0, q]$ dla każdego $q \in Q$
  • $[q, A, q_{m+1}] \to a[q_1, B_1, q_2] [q_2, B_2, q_3] \dots [q_m, B_m, q_{m+1}]$ dla dowolnych $q, q_1, \dots, q_{m+1} \in Q$, dla każdego $a \in \Sigma \cup \{\epsilon\}$ i dowolnych $A, B_1, \dots, B_m \in \Gamma$ takich, że $(q_1, B_1, \dots, B_m) \in \delta(q, a, A)$
  • $[q, A, p] \to a$ jeśli $(p, \epsilon) \in \delta(q, a, A)$.

Wyprowadzenie lewostronne w $G$ symuluje ruchy $M$ na wejściu $x$.

$[q, A, p]$ wyprowadza $x \iff M$ będąc w stanie $q$ i mając na stosie $A \alpha$ po wczytaniu $x$ znajdzie się w stanie $p$, na stosie będzie $\alpha$ i $\alpha$ nie była zmieniana i czytana w tym czasie.

Teraz dowód indukcyjny po liczbie kroków, że $$[q, A, p] \underset{G}{\Rightarrow}^* x \iff (q, x, A) \underset{M}{\vdash}^* (p, \epsilon, \epsilon)$$

6.2. Przykład

Mamy $M = \left( \{p,q\}, \{a,b\}, \{X,Z\}, \delta, p, Z, \emptyset \right)$

Możemy powyższą tabelkę zapisać w następujący sposób:

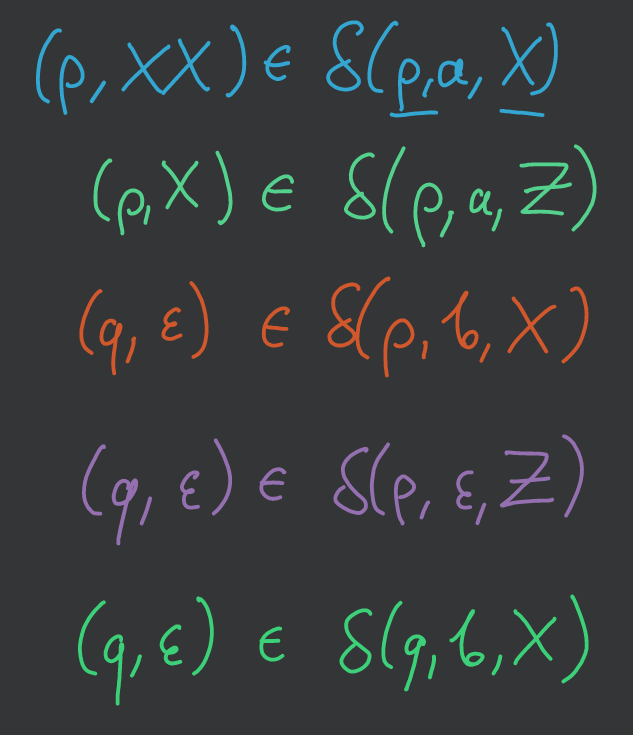
Tworzymy produkcje:

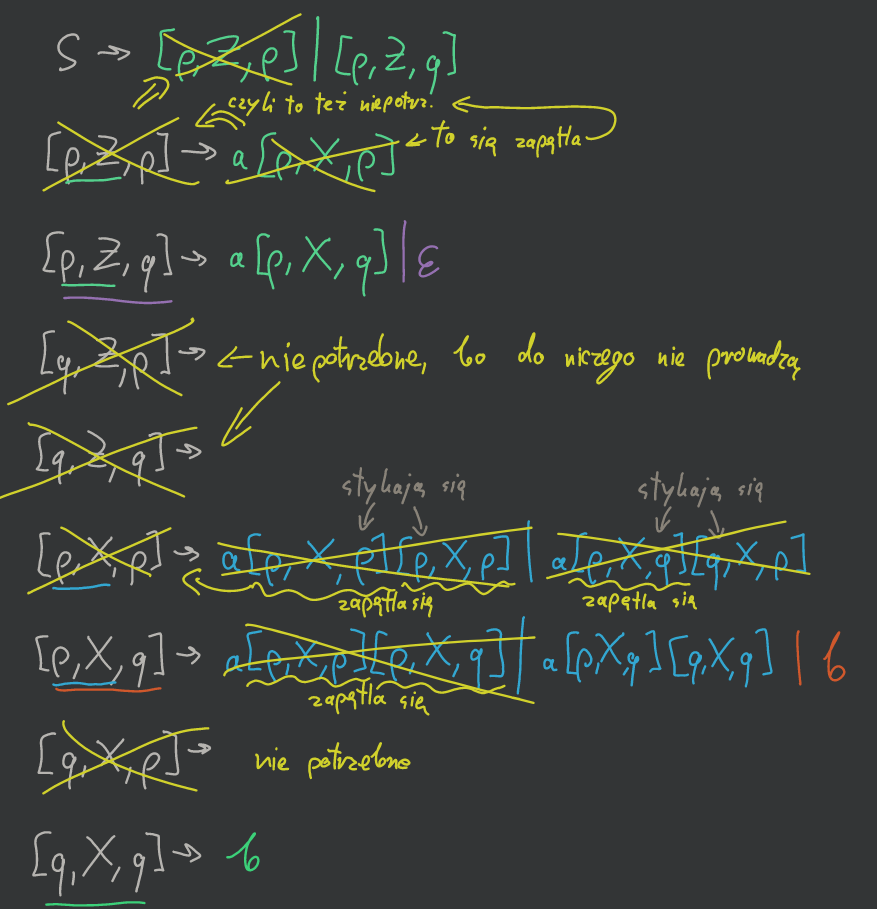
i od razu je „przetwarzamy” na podstawie funkcji przejścia $\delta$ i patrząc na dowód twierdzenia.
Następnie usuwamy niepotrzebne elementy, które albo się zapętlają, albo prowadzą do nikąd.