Przepływy w sieciach II

• Lemat A
  • D-d Lematu A
• Oznaczenie #1
• Wniosek #1 (Lemat B)
  • D-d Lematu B
• Twierdzenie (Ford-Fulkerson)
  • D-d Twierdzenia (Ford-Fulkerson)
• Metoda Forda-Fulkersona
  • Przykład (Metoda Forda-Fulkersona)
• Fakt #1
• Fakt #2
• Algorytm Edmontona-Karpa
• Twierdzenie #2
  • D-d Twierdzenia #2

Lemat A

Niech $(V,E,s,t,c)$ będzie siecią. Niech $f$ będzie przepływem w sieci.
Niech $X \subseteq V$ będzie takim zbiorem, że $s \in X$ oraz $t \notin X$.
Wówczas $$\lVert f \rVert = \mathrm{out}_f(X) - \mathrm{in}_f(X).$$

D-d Lematu A

Niech:

• $Y = X \setminus \{s\}$
• $a = f(\{s\}, X^\complement)$
• $b = f(\{s\}, Y)$
• $c = f(Y,\{s\})$
• $d = f(X^\complement, \{s\})$
• $e = f(Y, X^\complement)$
• $f = f(X^\complement, Y)$

Wtedy:

1. $\lVert f \rVert = (a+b) - (c+d)$
2. $e + c = f + b$ (bo $Y \cap \{s,t\} = \emptyset$)
3. $\mathrm{out}_f(X) - \mathrm{in}_f(X) = (a+e) - (d+f)$

Zatem $$\lVert f \rVert = (a-d) + (b-c) \\= (a-d) + (e-f) = (a+e) - (d+f) \\= \mathrm{out}_f(X) - \mathrm{in}_f(X).$$

Oznaczenie #1

Przepustowością cięcia $X$ (czyli takiego zbioru wierzchołków, że $s \in X$ oraz $t \notin X$) nazywamy liczbę $$c(X) = \sum \{c(e): \mathrm{fst}(e) \in X \land \mathrm{snd}(e) \in X^\complement \}$$

Wniosek #1 (Lemat B)

Niech $(V,E,s,t,c)$ będzie siecią. Niech $f$ będzie przepływem w sieci. Niech $X \subseteq V$ będzie takim zbiorem, że $s \in X$ oraz $t \notin X$. Wówczas $$\lVert f \rVert \le c(X)$$

D-d Lematu B

Korzystając z poprzedniego Lematu mamy $$\lVert f \rVert = \mathrm{out}_f(X) - \mathrm{in}_f(X) \\ \le \mathrm{out}_f(X) = \sum \{ f(e): \mathrm{fst}(e) \in X \land \mathrm{snd}(e) \in X^\complement \} \\ \le \sum \{ c(e): \mathrm{fst}(e) \in X \land \mathrm{snd}(e) \in X^\complement \} = c(X)$$

Uwaga: poprzedni fakt można zapisać następująco: $$\max \{ \lVert f \rVert: f \text{ jest przepływem} \} \le \min \{ c(X): X \text{ jest cięciem} \}$$

Twierdzenie (Ford-Fulkerson)

Niech $\mathcal{N}$ będzie siecią.
Wówczas $$\max \{ \lVert f \rVert: f \text{ jest przepływem } \mathcal{N} \} = \min \{ c(X): X \text{ jest cięciem w } \mathcal{N} \}$$

D-d Twierdzenia (Ford-Fulkerson)

Niech $f$ będzie przepływem o największej możliwej wartości $\lVert f \rVert$. Niech $X$ będzie zbiorem tych wszystkich wierzchołków $x$, że istnieje $f$–ścieżka powiększająca od $s$ do $x$. Wówczas $t \notin X$ (gdyby $t \in X$, to moglibyśmy powiększyć $f$). Jeśli $x \in X, y \in X^\complement$ oraz $(x,y) \in E$, to $f((x,y)) = c((x,y))$ (inaczej mielibyśmy $f$–ścieżkę powiększającą od $s$ do $y$). Podobnie, jeśli $x \in X, y \in X^\complement$ oraz $(y,x) \in E$, to $f((y,x)) = 0$ (inaczej mielibyśmy $f$–ścieżkę powiększającą od $s$ do $y$).
Zatem $$\lVert f \rVert = \mathrm{out}_f(X) = \mathrm{in}_f(X) = c(X) - 0 = c(X)$$

Source: Bela Bollobas, Modern Graph Theory, Springer, 1998

Metoda Forda-Fulkersona

f := 0;
WHILE istnieje f-ścieżka powiększająca
    P := jakaś ścieżka f-powiększająca;
    f := f poprawione o P
ENDWHILE

Uwaga: powyższy pseudokod nazywamy metodą, a nie algorytmem, bo nie określamy jak wybierać ścieżkę $f$–powiększającą

Przykład (Metoda Forda-Fulkersona)

Przykład sieci, dla której metoda ta działa bardzo długo:

Rozważamy prostą sieć z czterema wierzchołkami. Zaczynamy od potoku równego zero. Rozważamy dwie ścieżki powiększające: $P = (s,a,b,t)$ oraz $Q = (a,b,a,t)$

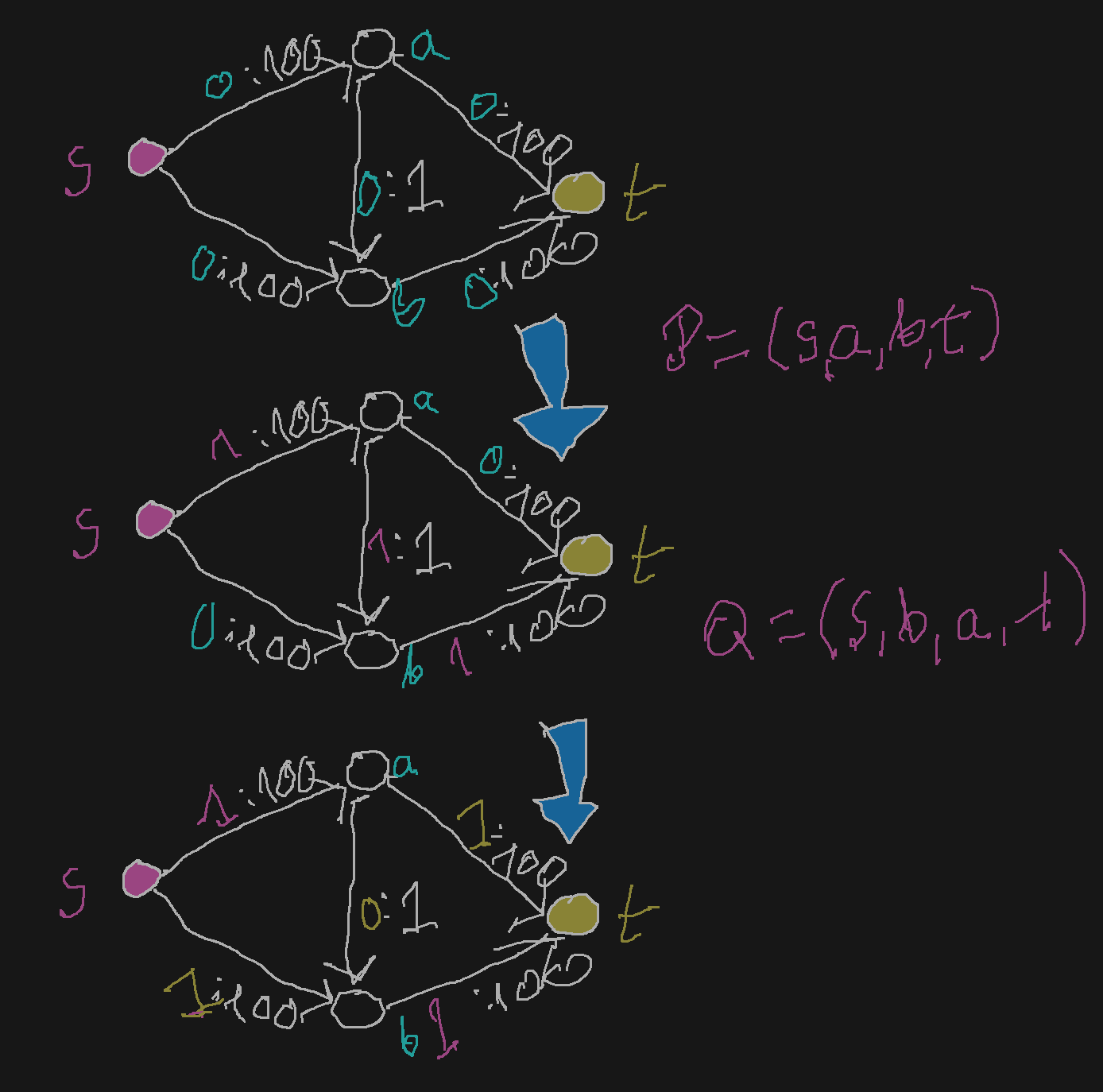
Po tych dwóch krokach przepustowość zwiększyliśmy o $2$. Po $98$ kolejnych krokach $P,Q,P,Q\dots,P,Q$ dojdziemy do przepływu o maksymalnej wartości równej $200$.
Zauważmy, że gdybyśmy stosowali inne ścieżki powiększające $(s,a,t)$ oraz $(s,b,t)$ to po dwóch krokach otrzymalibyśmy maksymalny przepływ.

Fakt #1

Jeśli funkcja ograniczeń przyjmuje wartości naturalne (czyli $c \in \mathbb{N}^E$), to metoda Forda-Fulkersona kończy swoje działanie po skończonej liczbie kroków.

Fakt #2

Jeśli $c$ przyjmuje wartości niewymierne, to może się zdarzyć (przy doborze „złośliwej” funkcji $c$), że metoda ta działa nieskończenie długo i, o zgrozo, nawet graniczny potok nie jest najlepszy!

Algorytm Edmontona-Karpa

f := 0
WHILE istnieje f-ścieżka powiększająca
    P := jakaś ścieżka f-powiększająca o najkrótszej (w sensie liczby wierzchołków) długości
    f := f poprawione o P
ENDWHILE

Twierdzenie #2

Algorytm Edmontona-Karpa kończy swoje działanie po skończonej liczbie kroków i zwraca przepływ o największej wartości.

D-d Twierdzenia #2

1. Wprowadźmy pojęcia grafu $f$-powiększającego: $$F_f = \\ \{ (x,y) \in E: f((x,y)) < c((x,y,)) \} \cup \\ \cup \left\{ (x,y): (y,x) \in E \land f((y,x)) > 0 \right\}$$ i definiujemy $d_f(x) = d_{G_f}(s,x)$.
2. Pokazujemy, że jeśli $f'$ jest potokiem otrzymanym z potoku $f$ przez zastosowanie ścieżki powiększającej o najkrótszej długości, to $d_f(x) \le d_{f'}(x)$ dla każdego wierzchołka $x$.
3. Definiujemy pojęcie krawędzi aktywnej na ścieżce powiększającej: jest to taka krawędź, na której zmieniamy wartość potoku. Zauważamy, że na każdej ścieżce musi być krawędzi aktywna.
4. Sprawdzamy, że jeśli krawędź $e = (x,y)$ była aktywna w krokach $i$ oraz $j$ i jednocześnie $i < j$ to $d_{f_j}(x) \ge d_{f_i}(x) + 2$.
5. Wnioskujemy, że krawędź może być aktywna co najwyżej $\frac{|V|}{2}$ razy.
6. Z tego wnioskujemy, że główna pętla może być wykonywana przez co najwyżej $\frac{|E|\cdot |V|}{2}$ razy.
7. To w zasadzie wystarcza. Ale można się zastanowić nad złożonością pod-procedury wyznaczania ścieżek powiększających. Graf $G_f$ ma co najwyżej $2|E|$ krawędzi. Algorytm przeszukiwania wszerz wykonywany jest w czasie $O(|V| + |E|)$.
   Zatem złożoność algorytmu można oszacować przez $O\left(\left(|V| + |E|\right) \cdot |V| \cdot |E| \right)$. Można to zrobić lepiej – więcej w source. Dla nas ważne jest to, że algorytm ten działa w czasie wielomianowym od $|V|$ i $|E|$.

Source: CLRS