Grafy skierowane

• $\text {Def}$ Graf skierowany
• $\text {Twierdzenie}$ #1
  • D-d $\text {Twierdzenia}$ #1
• $\text {Def}$ Szkielet
• $\text {Fakt}$ #1
• $\text {Fakt}$ #2
• $\text {Def}$ Skierowany graf eulerowski
• $\text {Def}$ Silnie spójny graf
• $\text {Def}$ Kondensacja
• $\text {Twierdzenie}$ #2
• $\text {Def}$ Źródło/ Odpływ
• $\text {Twierdzenie}$ #3
  • D-d $\text {Twierdzenia}$ #3
• $\text {Def}$ Graf orientowalny
• $\text {Twierdzenie}$ #4

$\text {Def}$ Graf skierowany

Graf skierowany (digraf $\impliedby$ directed graph):
$G = (V,E,\varphi)$, gdzie $\varphi: E\to V\times V$.
Zbiór $V$ nazywamy zbiorem wierzchołków, zbiór $E$ nazywamy zbiorem krawędzi skierowanych.

1. Oznaczenia: jeśli $e \in E$ oraz $\varphi(e) = (x,y)$, to $\mathrm{fst}(e) = x$ (ogon $e$) oraz $\mathrm{snd}(e) = y$ (głowa $e$)
2. (stopień wyjściowy, outdegree) $\deg^+(v) = |\{e\in E: \mathrm{fst}(e) = x\}|$
3. (stopień wejściowy, indegree) $\deg^-(v) = |\{e\in E: \mathrm{snd}(e) = x\}|$
4. Ścieżką w grafie skierowanym nazywamy ciąg $x_0,e_1,x_1,e_2,\dots,e_n,x_n$ taki, że $x_0,\dots,x_n$ są wierzchołkami, $e_1,\dots,e_n$ są krawędziami oraz dla każdego $i \in \{1,\dots,n\}$ mamy $\mathrm{fst}(e_i) = x_{i-1}$ i $\mathrm{snd}(e_i) = x_i$

$\text {Twierdzenie}$ #1

$$\sum_{v\in V}\deg^+(v) = |E| \\ \sum_{v\in V}\deg^-(v) = |E|$$

D-d $\text {Twierdzenia}$ #1

$$|E| = \sum_{v\in V}|\{e\in E: \mathrm{fst}(e) = v\}| = \sum_{v\in V}\deg^+(v).$$

$\text {Def}$ Szkielet

Szkieletem (underlying graph) grafu skierowanego $G$ nazywamy graf $G^* = (V,E,\varphi^*)$, gdzie $\varphi^*(e) = \{x,y\}$ jeśli $\varphi(e) = (x,y) \lor \varphi(e) = (y,x)$.

$\text {Fakt}$ #1

Jeśli $G^*$ jest szkieletem digrafu $G$ i $x \in V(G)$ to: $$\deg_{G^*}(x) = \deg^+_G(x) + \deg^-_G(x)$$

$\text {Fakt}$ #2

Graf skierowany nazywamy spójnym jeśli jego szkielet jest spójny.

$\text {Def}$ Skierowany graf eulerowski

Skierowanym grafem eulerowskim nazywamy taki graf, w którym istnieje ścieżka zamknięta (początek równa się końcowi) która przechodzi przez wszystkie krawędzie.
Klasyczne twierdzenie Eulera bez trudu przenosi się na grafy skierowane: są to grafy spójne takie, że $(\forall v\in V)(\deg^-(v) = \deg^+(v))$. Wynika to z faktu, że do z każdego wierzchołka chcemy wyjść tyle samo razy jak i do niego wejść. Jeśli $\deg^-(v) \neq \deg^+(v)$ wówczas w wierzchołku $v$ możemy utknąć lub też pominąć jedną z krawędzi.

//TODO: Sformułuj pojęcie grafu pół-eulerowskiego, sformułuj twierdzenie charakteryzujące grafy pół-eulerowskie i udowodnij je.

$\text {Def}$ Silnie spójny graf

Graf jest silnie spójny, jeśli dla każdej pary wierzchołków $x,y$ istnieje ścieżka od $x$ do $y$. Podzbiór $X$ $\subseteq E$ jest silnie spójny jeśli obcięcie grafu $G$ do $X$ jest grafem silnie spójnym. Silnie spójną składową nazywamy maksymalny w sensie inkluzji silnie spójny podzbiór zbioru wierzchołków.

$\text {Def}$ Kondensacja

Kondensacja grafu skierowanego: ustalamy digraf $G=(V,E,\varphi)$

1. Definiujemy $x\gg y \equiv$ istnieje (skierowana) ścieżka od $x$ do $y$
2. Definiujemy $(x \equiv y) \leftrightarrow \big((x\gg y) \land (y\gg x)\big)$
3. Pokazujemy, że relacja $\equiv$ jest relacją równoważności na $V$
4. Pokazujemy, że klasy abstrakcji relacji $\equiv$ pokrywają się z silnie spójnymi składowymi
5. Na $V_{/\equiv}$ definiujemy: $$E' = \{(C_1, C_2): (\exists e\in E)(\mathrm{fst}(e) \in C_1 \land \mathrm{snd}(e) \in C_2)\}$$

Graf $(V_{/\equiv}, E')$ nazywamy kondensacją grafu $G$.

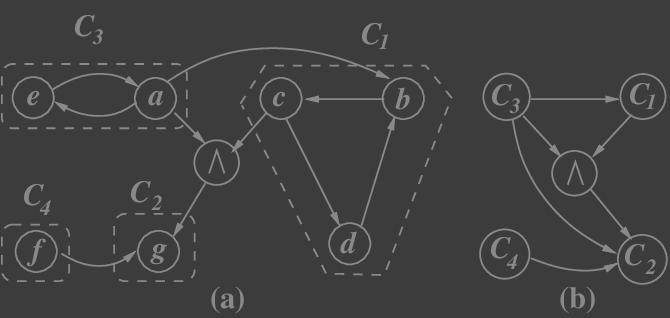
Do znajdowania silnie spójnych składowych można się posłużyć algorytmem Kosaraju lub algorytmem Tarjana.

$\text {Twierdzenie}$ #2

Kondensacja grafu $G$ jest skierowanym grafem acyklicznym (DAG).

$\text {Def}$ Źródło/ Odpływ

Źródło to taki wierzchołek $v$, że $\deg^-(v) = 0$.

Odpływ to taki wierzchołek $v$, że $\deg^+(v) = 0$.

$\text {Twierdzenie}$ #3

W każdym skończonym DAGu istnieje źródło i istnieje odpływ.

D-d $\text {Twierdzenia}$ #3

Bierzemy skierowaną drogę o największej długości; pokazujemy, że jej początek jest źródłem a końcowy wierzchołek jest odpływem.

$\text {Def}$ Graf orientowalny

Graf $G$ jest orientowalny jeśli istnieje graf skierowany o zbiorze wierzchołków $V(G)$ którego szkieletem jest $G$.

$\text {Twierdzenie}$ #4

Graf $G$ jest orientowalny iff, gdy jest spójny i nie zawiera mostu (czyli jest spójny i każda krawędź leży na cyklu).