Grafy planarne III i spójność

• Kontrakcja krawędzi grafu
  • Kontrakcja grafu Petersena
• $\text {Fakt}$ #1
• $\text {Definicja}$ Minor grafu
• $\text {Twierdzenie}$ Wagnera
• $K_{3,3}$ na torusie
  • Eliminacja jedno przecięcia grafu $K_{3,3}$
  • Topologiczna transformacja powierzchni
  • Powierzchnie orientowalne o małych „genusach”
• $\text {Definicja}$ Genus grafu
  • $\text {Fakt}$ Każdy graf (skończony) ma określony genus
• $\text {Twierdzenie}$ #2
• $\text {Fakt}$ #3
  • D-d $\text {Faktu}$ #3
• $\text {Definicja}$ Spójność wierzchołkowa grafu spójnego
• $\text {Definicja}$ spójność krawędziowa grafu spójnego
• $\text {Twierdzenie}$ #3
  • D-d $\text {Twierdzenia}$ #3
• $\text {Definicja}$ $(A,B)$–ścieżka
• $\text {Definicja}$ $(A,B)$–konektor
• $\text {Definicja}$ $(A,B)$–separator

Kontrakcja krawędzi grafu

Niech $(V, E, \varphi)$ będzie grafem i $e \in E$
Niech $\varphi(e) = \{a,b\}$

Kontrakcją grafu $G$ względem krawędzi $e$ nazywamy graf $G/e$

• ze zbiorem wierzchołków $(V \setminus \{x,y\}) \cup \{w\}$ (gdzie $w$ jest jakimś elementem nie należącym do $V$)
• ze zbiorem krawędzi $E \setminus \{e\}$
• funkcją incydencji $\varphi'$ określoną wzorem $$\varphi'(f) = \begin{cases} \{x,w\} & \varphi(f) = \{x,a\} \lor \varphi(f) = \{x,b\}\\ \varphi(f) & \text{otherwise}\\ \end{cases}$$ Uwaga: formalna definicja jest nieco zawiła, ale intuicja jest prosta: krawędź $\{a,b\}$ ściągamy do jednego wierzchołka.

Kontrakcja grafu Petersena

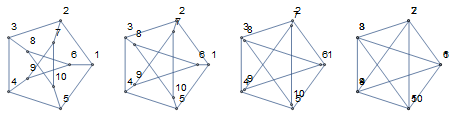
$\text {Fakt}$ #1

Następujące operacje nie zmieniają planarności grafów:

• usunięcie wierzchołka
• usunięcie krawędzi
• kontrakcja krawędzi

$\text {Definicja}$ Minor grafu

Graf $G$ jest minorem grafu $H$ ($G \preceq H$) jeśli $G$ może być otrzymany z grafu $H$ za pomocą skończonej liczby operacji usunięcia wierzchołka, usunięcia krawędzi lub kontrakcji krawędzi.

$\text {Twierdzenie}$ Wagnera

Graf nie jest planarny $\iff$ $(K_{3,3} \preceq G \lor K_5 \preceq G)$

$K_{3,3}$ na torusie

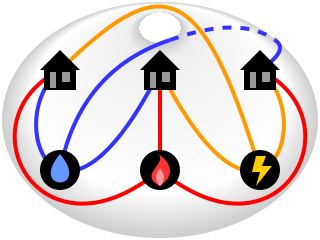
Eliminacja jedno przecięcia grafu $K_{3,3}$

Topologiczna transformacja powierzchni

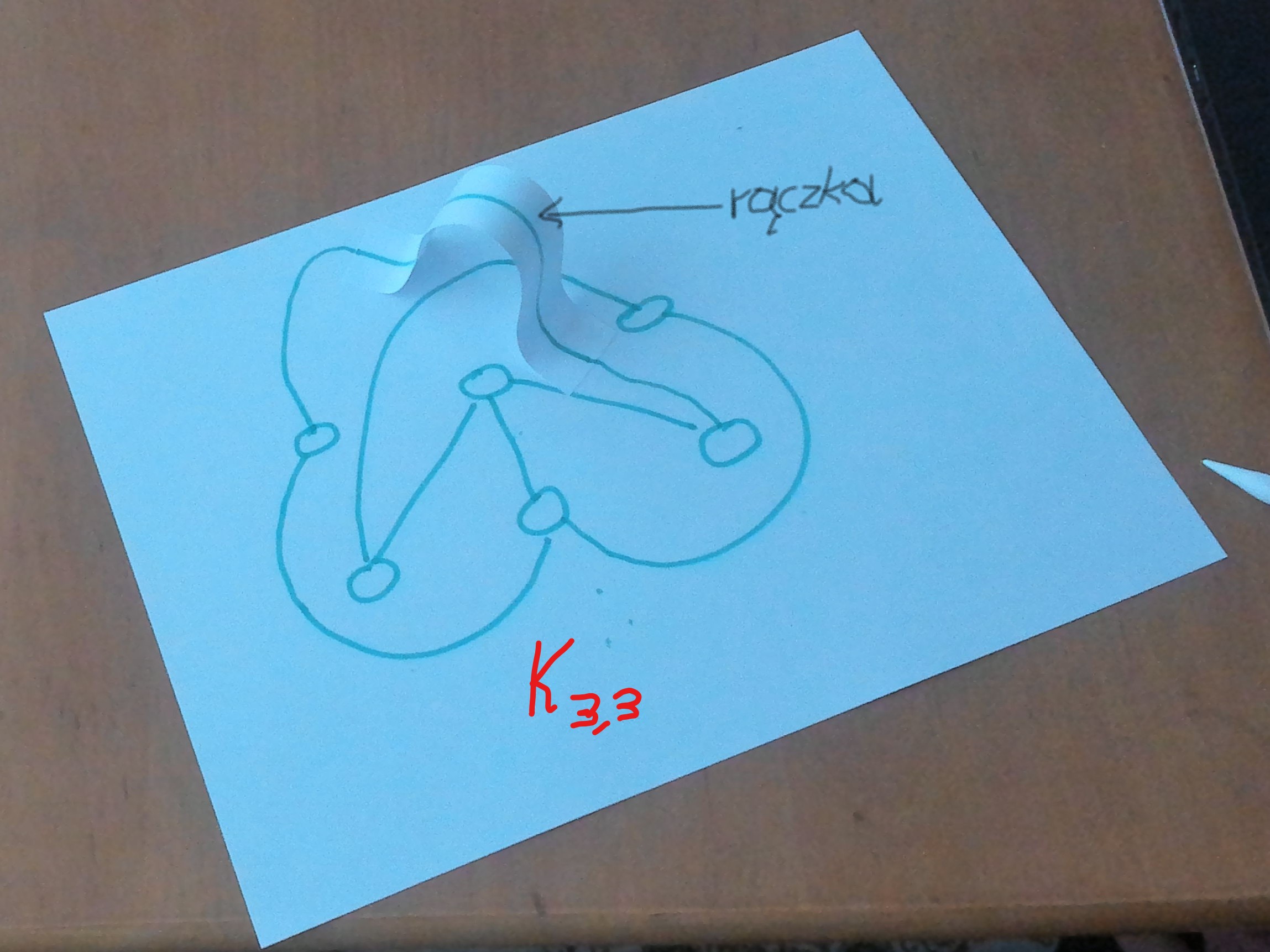
Powierzchnie orientowalne o małych „genusach”

$\text {Definicja}$ Genus grafu

Genus Grafu = minimalna liczba rączek, które należy dodać do płaszczyzny (lub sfery) potrzebnych do narysowania grafu na tej powierzchni „bez przecięć”.

$\text {Fakt}$ Każdy graf (skończony) ma określony genus

$\text {Twierdzenie}$ #2

Jeśli graf ma genus $g$ to $$F - E + V = 2 - 2 \cdot g$$

$\text {Fakt}$ #3

Jeśli graf $(V,E)$ jest spójny, $n = |V| \ge 2$ i nie jest grafem pełnym, to istnieje zbiór $X \subseteq V$ taki, że $|X| = n-2$ i $G \setminus X$ nie jest spójny.

D-d $\text {Faktu}$ #3

Załóżmy, że $a,b \in V$, $a \neq b$ oraz $\{a, b\} \notin E$. Kładziemy $X = V\setminus \{a, b\}$ i mamy $G \setminus X = (\{a,b\}, \emptyset)$.

$\text {Definicja}$ Spójność wierzchołkowa grafu spójnego

Mamy graf spójny $G = (V,E)$. Spójność wierzchołkowa $G$: $$\kappa(G) = \begin{cases} n-1 & : G \sim K_n \\ \min\{|X|: X \subseteq V \land G\setminus X ~\text{nie jest spójny}\} & : \text{nie jest zupełny} \end{cases}$$ Uwaga: z powyższego faktu wynika, że dla dowolnego spójnego grafu prostego $(V,E)$ mamy $\kappa(G) \le |V| - 1$;
co więcej: $\kappa(G) = |V| - 1$ $\iff$ graf jest grafem zupełnym

$\text {Definicja}$ spójność krawędziowa grafu spójnego

Mamy graf spójny $G = (V,E)$. Spójność krawędziowa $G$: $$\lambda(G) = \min\{|Y|: Y \subseteq E \land G\setminus Y ~\text{nie jest spójny}\}$$

$\text {Twierdzenie}$ #3

Dla dowolnego grafu spójnego $G = (V,E)$ takiego, że $|V| \ge 2$ mamy $\kappa(G) \le \lambda(G)$.

D-d $\text {Twierdzenia}$ #3

Niech $E'$ będzie zbiorem krawędzi takim, że $G\setminus E'$ nie jest spójny oraz, że $|E'| = \lambda(G)$. Wtedy $G\setminus E'$ ma dwie składowe spójne (dowolna krawędź z $E'$ uspójnia $G\setminus E'$). Oznaczmy je przez $S$ oraz $\overline{S}$.

Zauważmy, że $(\forall x\in S)(\forall y \in \overline{S})(\{x,y\} \in E \rightarrow \{x,y\} \in E')$.
Jeśli $(\forall x\in S)(\forall y\in \overline{S})(\{x,y\} \in E)$, to $\lambda(G) = |S| \cdot |\overline{S}| = |S|(|V| - |S|) \ge |V| - 1$
Ale $\kappa(G) \le |V| - 1$, więc w tym przypadku dowodzona nierówność jest prawdziwa.

Załóżmy więc, że są $a \in S$ oraz $b \in \overline{S}$ takie, że $\{a,b\} \notin E$.
Niech $T_1 = \{y \in \overline{S}: \{a,y\} \in E\}$, $T_2 = \{x \in S\setminus\{a\}: (\exists y\in \overline{S})(\{x,y\}\in E\}$.
Niech $T = T_1 \cu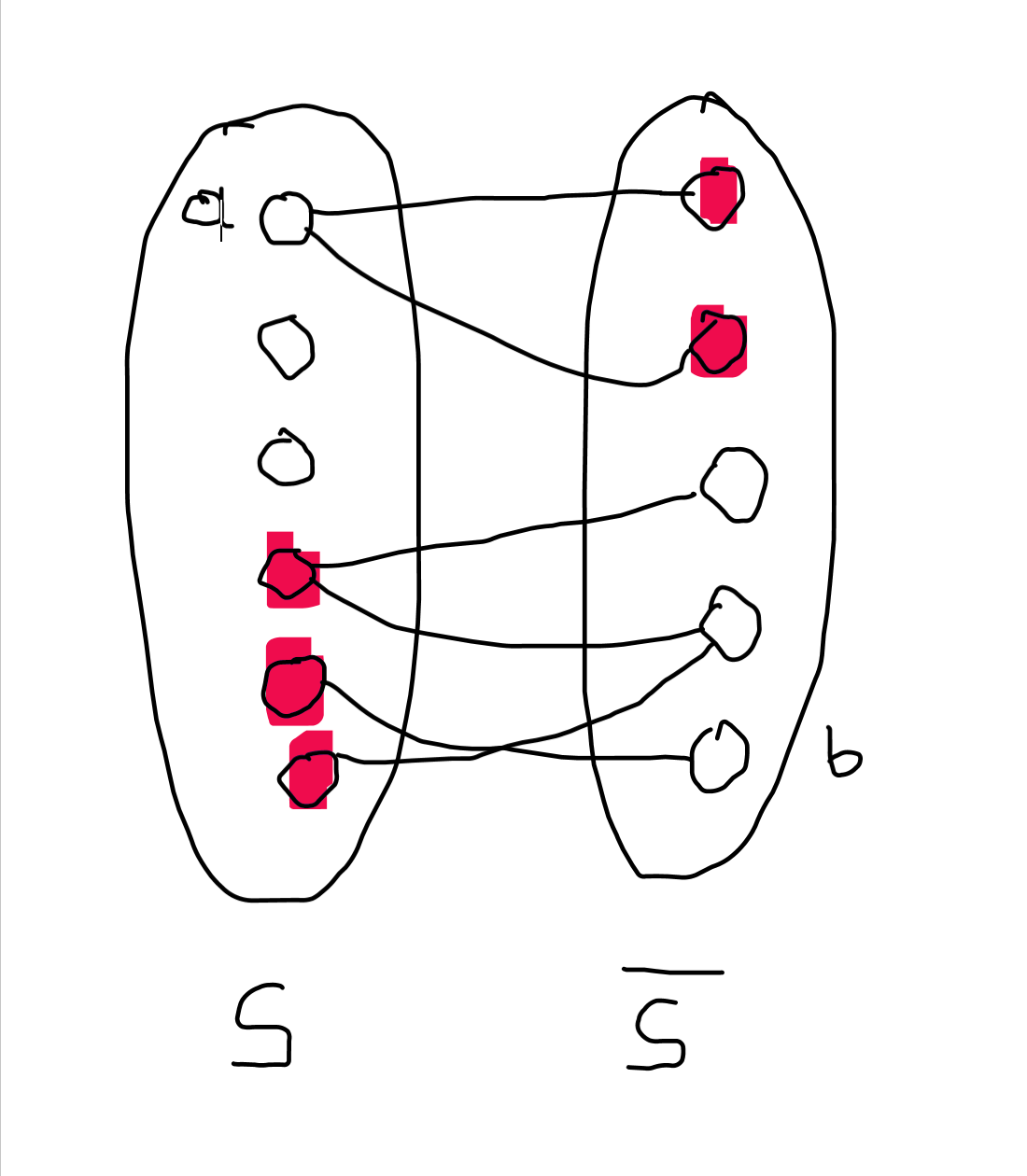p T_2$ Zauważmy, że $b\in\overline{S}\setminus T$ oraz $a\in S\setminus T$. Usuwając wierzchołki ze zbioru $T$ usuwamy wszystkie krawędzie ze zbioru $E'$. Zbiór $T$ jest więc zbiorem rozspajającym (wierzchołki $a$ i $b$ leżą w różnych komponentach spójnych $G\setminus T$). Ponadto $|T| \le |E'|$.
Zatem $\kappa(G) \le |E'| = \lambda(G)$.

$\text {Definicja}$ $(A,B)$–ścieżka

Niech $A,B \subseteq V$. $(A,B)$–ścieżką nazywamy drogę $x_0,x_1,\dots,x_{n-1},x_n$ w grafie taką, że $x_0 \in A$, $x_n \in B$ oraz $\{x_1,\dots,x_{n-1}\} \cap (A\cup B) = \emptyset$.

Uwaga: jeśli $A\cap B \neq \emptyset \land c \in A\cap B$, to ciąg ($c$) jest $(A,B)$–ścieżką długości $0$.

$\text {Definicja}$ $(A,B)$–konektor

Niech $A,B \subseteq V$. $(A,B)$–konektorem nazywamy dowolny zbiór parami rozłącznych $(A,B)$–ścieżek.

$\text {Definicja}$ $(A,B)$–separator

Niech $A,B \subseteq V$. $(A,B)$–separatorem nazywamy dowolny zbiór wierzchołków $X$, taki, że dla dowolnej $(A,B)$–ścieżki $P$ mamy $P\cap X \neq \emptyset$.