Grafy Planarne I

by Jerry Sky

2020-04-01

Kilka pojęć pomocniczych

Krzywa w Rn\reals^n

Dowolne ciągłe odwzorowanie γ:[a,b]→Rn\gamma:[a,b] \rightarrow \reals^n

Krzywa Jordana

taka krzywa γ:[a,b]→Rn\gamma:[a,b] \rightarrow \reals^n, że γ(a)=γ(b)\gamma(a) = \gamma(b) oraz, że γ\gamma jest różnowartościowe na przedziale (a,b)(a,b).

Wyobrażać ją sobie możemy jako pętlę bez przecięć.

TwierdzenieTwierdzenie o krzywej Jordana

Każda krzywa Jordana rozdziela płaszczyznę na dwa rozłączone obszary i jest ich wspólnym brzegiem.

Jordan’s curve

Definicja\text{Definicja} graf planarny

Graf G=(V,E)G=(V,E) jest grafem planarnym jeśli jego wierzchołki możemy przedstawić jako punkty płaszczyzny, a krawędzie jako krzywe na płaszczyźnie łączące wierzchołki, przy czym punktami wspólnymi dwóch różnych krawędzi mogą być tylko ich końcowe wierzchołki.

Poniżej widzimy, że graf K4K_4 jest grafem planarnym.

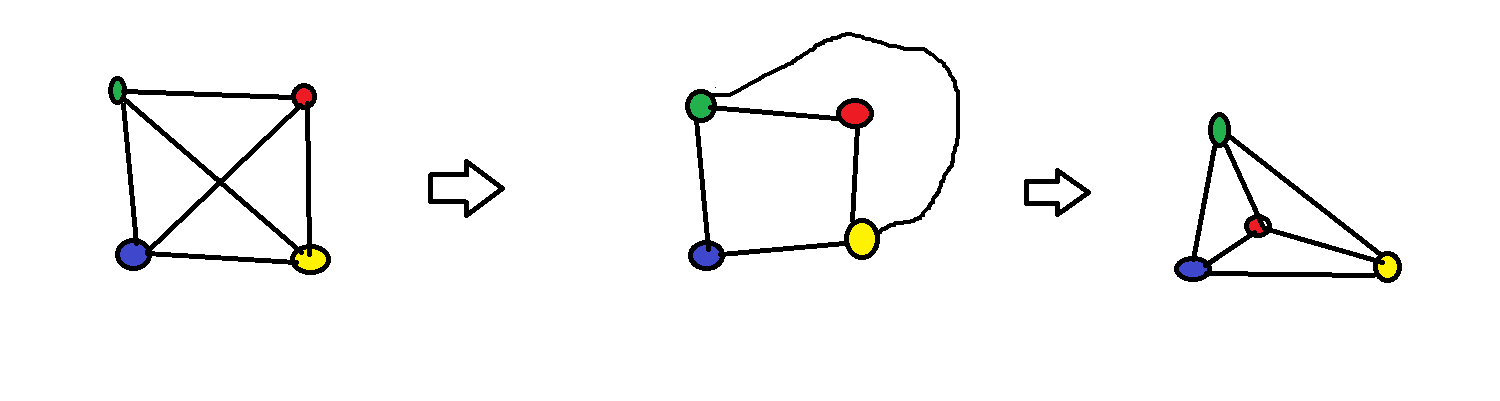
graf planarny

Graf K2,4K_{2,4} również jest planarny.

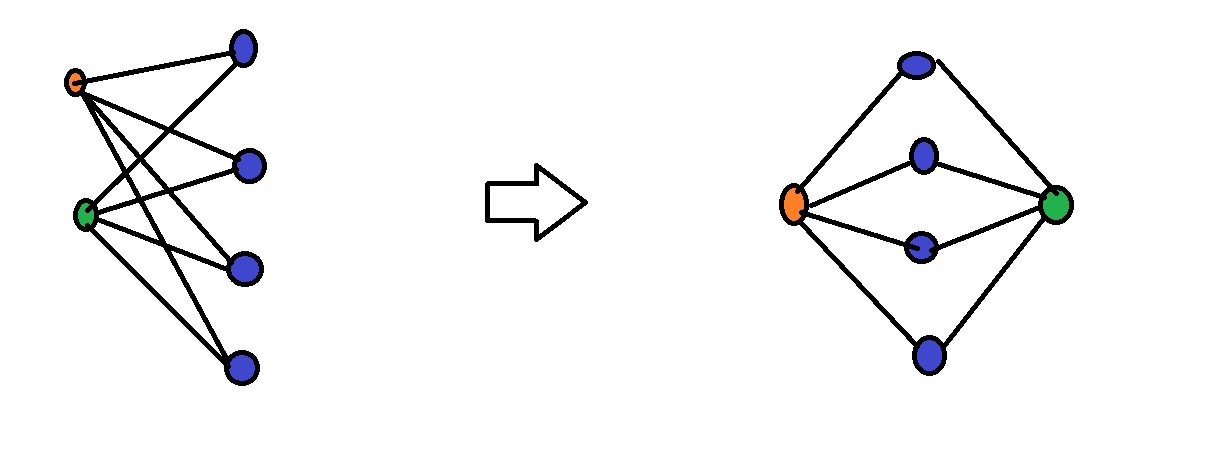
graf planarny

Uwagi\text{Uwagi} co do grafów planarnych

  1. Dosyć łatwo można pokazać, że w pojęciu planarności pojęcie łuku można zastąpić krzywymi łamanymi, czyli takimi, które rozbijają się na skończoną liczę odcinków. Od tej pory zawsze będziemy stosowali takie reprezentacje grafów planarnych.
  2. Można również pokazać, że dowolne krzywe można zastąpić odcinkami. Widzieliśmy to na dwóch powyższych rysunkach.

Twierdzenie\text{Twierdzenie} Grafy K3,3K_{3,3} oraz K5K_5 nie są planarne

Nieformalny dowód K3,3K_{3,3} jest nie-planarny

Udowodnimy to TwierdzenieTwierdzenie w późniejszej części tego wykładu.

Reprezentacja planarna grafu

Niech GG będzie zbiorem punktów i krawędzi.
Jest to zbiór domknięty.
Zbiór R2∖G\reals^2 \setminus G rozkłada się na spójne składowe zwane regionami (ścianami):

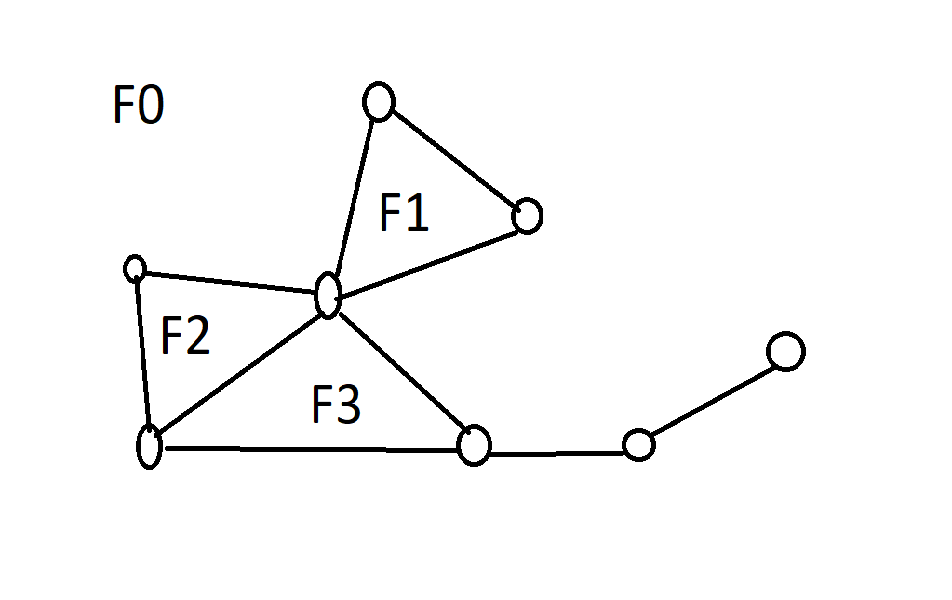
reprezentacja planarna grafu

Przykładowo, tutaj mamy 4 regiony (ściany) przy czym region F0F_0 jest nieograniczony.

W przypadku drzewa istnieje tylko jeden region (ściana):

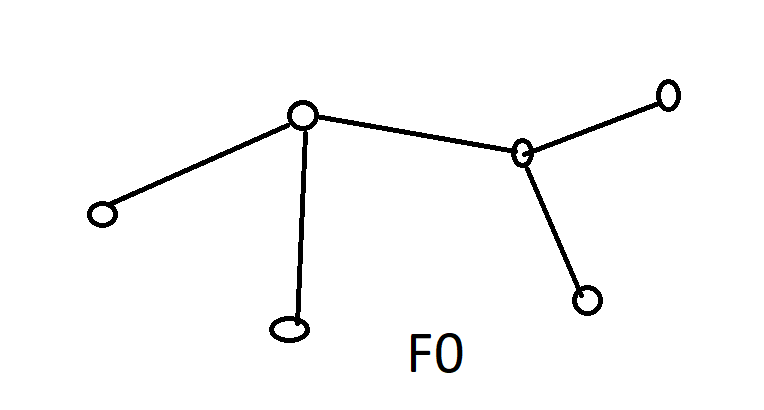
drzewo

Twierdzenie\text{Twierdzenie} Eulera

Niech FF oznacza liczbę regionów (ścian), EE liczbę krawędzi oraz VV liczbę wierzchołków spójnego grafu planarnego.
Wówczas mamy F−E+V=2F - E + V = 2.

D-d Twierdzenia\text{Twierdzenia} Eulera

Ustalmy liczbę VV. Dowód robimy indukcją po liczbie krawędzi. Ze spójności grafu wynika, że E≥V−1E \ge V-1.

Jeśli E=V−1E=V-1, to graf jest drzewem, nie ma więc cyklu, więc ma tylko jeden region (ścianę). Oczywiście wówczas mamy faktycznie F−E+V=1−(V−1)+V=2 F - E + V = 1 - (V-1) + V = 2

Załóżmy więc, że E>V−1E>V-1. Wtedy graf ma cykl. Niech ee będzie krawędzią z tego cyklu. Krawędź ee leży na brzegu dwóch ścian (jedną z nich może być region nieograniczony).
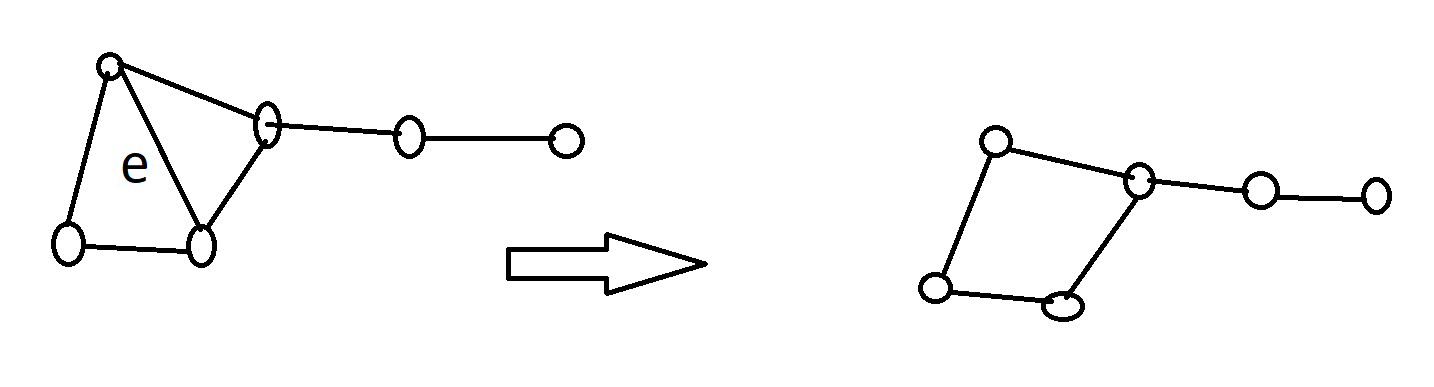
Usuńmy ee z grafu: d-d Euler

Liczba EE zmalała o jeden, liczba FF zmalała o jeden, a liczba VV nie uległa zmianie. Wartość wyrażenia F−E+VF - E + V nie uległa więc zmianie. Więc jest nadal równa 22.

Wniosek z Twierdzenia\text{Twierdzenia} Eulera

Wszystkie planarne realizacje grafu spójnego mają taką samą liczbę ścian.

Twierdzenie\text{Twierdzenie} liczba krawędzi w planarnym grafie

Niech GG będzie prostym grafem planarnym V≥3V\ge3.
Wówczas E≤3⋅V−6 E \le 3\cdot V - 6 a jeśli graf nie zawiera trójkątów to E≤2⋅V−4 E \le 2\cdot V - 4

D-d Twierdzenia\text{Twierdzenia} liczba krawędzi w planarnym grafie

  1. Ogólnie (kiedy mamy trójkąty)
    1. Zauważmy, że każdy region (ściana) ograniczony jest co najmniej trzema krawędziami. Zauważmy również, że każda krawędź leży na brzegu co najwyżej dwóch regionów (ścian). Zatem 3⋅F≤2⋅E 3 \cdot F \le 2 \cdot E Zróbmy dokładniej:
      1. Niech F1,…,FyF_1,\dots,F_y będą regionami (ścianami).
      2. Niech fi, i=1,…,yf_i,~i=1,\dots,y oznacza liczbę krawędzi na regionie (ścianie) FiF_i.
      3. Niech e1,…,eme_1,\dots,e_m będą krawędziami
      4. Wówczas mamy 3⋅F=3⋅y≤∑i=1yfi=∑i=1y∑j=1m∥ej jest incyndentna z fj∥=∑j=1m∑i=1y∥ej jest incydentna z fj∥≤∑j=1m=2⋅m=2⋅E 3 \cdot F = 3 \cdot y \le \sum_{i=1}^{y}f_i = \sum_{i=1}^{y}\sum_{j=1}^{m}\lVert e_j~\text{jest incyndentna z}~f_j\rVert=\\ \sum_{j=1}^{m}\sum_{i=1}^{y}\lVert e_j~\text{jest incydentna z}~f_j\rVert \le \sum_{j=1}^{m} = 2\cdot m = 2\cdot E
    2. Użyjmy równości Eulera 2=F−E+V2 = F - E + V
    3. Pomnóżmy ją przez 33 i zastosujmy poprzednią nierówność 6=3F−3E+3V≤2E−3E+3V=−E+3V 6 = 3F - 3E + 3V \le 2E - 3E + 3V = -E + 3V dowód dr Sarada Herke
  2. W przypadku kiedy nie mamy trójkątów
    1. Zauważmy, że każdy region (ściana) ograniczony jest co najmniej czterema krawędziami. Zauważmy również, że każda krawędź leży na brzegu co najwyżej dwóch regionów (ścian). Zatem 4⋅F≤2⋅E 4 \cdot F \le 2 \cdot E Zróbmy dokładniej:
      1. Niech F1,…,FyF_1,\dots,F_y będą regionami (ścianami).
      2. Niech fi, i=1,…,yf_i,~i=1,\dots,y oznacza liczbę krawędzi na regionie (ścianie) FiF_i.
      3. Niech e1,…,eme_1,\dots,e_m będą krawędziami
      4. Wówczas mamy 4⋅F=4⋅y≤∑i=1yfi=∑i=1y∑j=1m∥ej jest incyndentna z fj∥=∑j=1m∑i=1y∥ej jest incydentna z fj∥≤∑j=1m=2⋅m=2⋅E 4 \cdot F = 4 \cdot y \le \sum_{i=1}^{y}f_i = \sum_{i=1}^{y}\sum_{j=1}^{m}\lVert e_j~\text{jest incyndentna z}~f_j\rVert=\\ \sum_{j=1}^{m}\sum_{i=1}^{y}\lVert e_j~\text{jest incydentna z}~f_j\rVert \le \sum_{j=1}^{m} = 2\cdot m = 2\cdot E
    2. Użyjmy równości Eulera 2=F−E+V2 = F - E + V
    3. Pomnóżmy ją przez 44 i zastosujmy poprzednią nierówność 8=4F−4E+4V≤ 2E−4E+4V=−2E+4V4≤ −E+2VE≤ 2V−4 \begin{aligned} 8 = 4F - 4E + 4V \le&~ 2E - 4E + 4V = -2E + 4V\\ 4 \le&~ -E + 2V\\ E \le&~ 2 V - 4 \end{aligned}

Wniosek Twierdzenia\text{Twierdzenia} liczba krawędzi w planarnym grafie

Liczba krawędzi w grafie planarnym jest dosyć mała, bo ograniczyć ją można przez 3V3V, czyli jest rzędu O(V)O(V) - to bardzo przydaje się w geometrii obliczeniowej.

Graf K5K_5 nie jest planarny

Gdyby był planarny to 10=E≤3V−6=3⋅5−6=910 = E \le 3V - 6 = 3\cdot 5 - 6 = 9.

Graf K3,3K_{3,3} nie jest planarny

Gdyby był planarny to 9=E≤2V−4=2⋅6−4=89 = E \le 2V - 4 = 2 \cdot 6 - 4 = 8.

Twierdzenie\text{Twierdzenie} #1

Załóżmy, że G=(V,E)G = (V,E) jest grafem planarnym. Wtedy istnieje wierzchołek vv taki, że deg⁡(v)≤5\deg(v) \le 5

Ta własność przyda nam się, gdy będziemy zajmowali się kolorowaniem grafów.

D-d Twierdzenia\text{Twierdzenia} #1

Załóżmy, że (∀v∈V)(deg⁡(v)≥6)(\forall v\in V)(\deg(v) \ge 6).
Wówczas 6⋅∣V∣≤∑v∈Vdeg⁡(V)=2⋅E≤2⋅(3⋅∣V∣−2)=6⋅∣V∣−6 6 \cdot \lvert V\rvert \le \sum_{v\in V} \deg(V) = 2\cdot E \le 2\cdot (3 \cdot \lvert V \rvert -2) = 6 \cdot \lvert V \rvert - 6 Otrzymaliśmy więc sprzeczność.