Przykładowe zastosowanie — Plane Trees

• 1. Drzewa uporządkowane
• 2. Klasa kombinatoryczna
  • 2.1. OGF

1. Drzewa uporządkowane

Drzewa takie, w których zachowujemy orientację całego drzewa

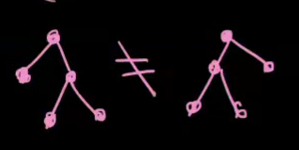
i dokładną pozycję każdego z węzłów.

Nie chodzi nam o drzewa w rozumieniu grafów.

Lista możliwych drzew dla liczby węzłów $[0;4]$:

2. Klasa kombinatoryczna

Spójrzmy na drzewa uporządkowane nieco „z góry”:

Można zauważyć, że każde drzewo jest zbudowane z korzenia oraz z pewnej liczby poddrzew.

Czyli mamy: $$\mathcal{T} \cong \mathcal{Z} \times \operatorname{SEQ}(\mathcal{T})$$

Możemy też podejść do sprawy nieco inaczej:
$T^{(i)}$ — klasa drzew o głębokości $<i$

• $T^{(1)} = \mathcal{Z} \times \operatorname{SEQ}(\emptyset)$
• $T^{(2)} = \mathcal{Z} \times \operatorname{SEQ}(\mathcal{T}^{(1)})$
• $T^{(3)} = \mathcal{Z} \times \operatorname{SEQ}(\mathcal{T}^{(2)})$

wizualnie:

• $\mathcal{T}^{(i)} \subseteq \mathcal{T}^{(i+1)}$
• $\bigcup_{i=1}^{\infty} \mathcal{T}^{(i)} \cong \lim_{i\to\infty} \mathcal{T}^{(i)}$
• $\lim_{i\to \infty} T^{(i)}(z) = T(z)$

2.1. OGF

Jednakże do liczenia OGF użyjemy tej pierwszej metody: $$\mathcal{T} \cong \mathcal{Z} \times \operatorname{SEQ}(\mathcal{T})$$

czyli mamy OGF: $T(z) = z \cdot \frac{1}{1 - T(z)}$

• $T(z)(1-T(z)) = z$
• $(T(z))^2 - T(z) + z = 0$
  • $\bold{T(z) = \frac{1}{2}\left( 1 - \sqrt{1 - 4z} \right)}$
  • $\sout{T(z) = \frac{1}{2}\left( 1 + \sqrt{1 - 4z} \right)}$

Mamy też coś takiego: $\sqrt{1 - 4z} = \sum_{n=0}^\infty (4z)^n \cdot \binom{\frac{1}{2}}{n} = \sum_{n=0}^\infty \frac{1}{n} \binom{2n - 2}{n-1} \cdot z^n$

Sprawdźmy dla $n=4$:
$\frac{1}{4} \cdot \binom{6}{3} = 5$
i to się zgadza z tym, co otrzymaliśmy wcześniej