1. DEF: Funkcja wypukła
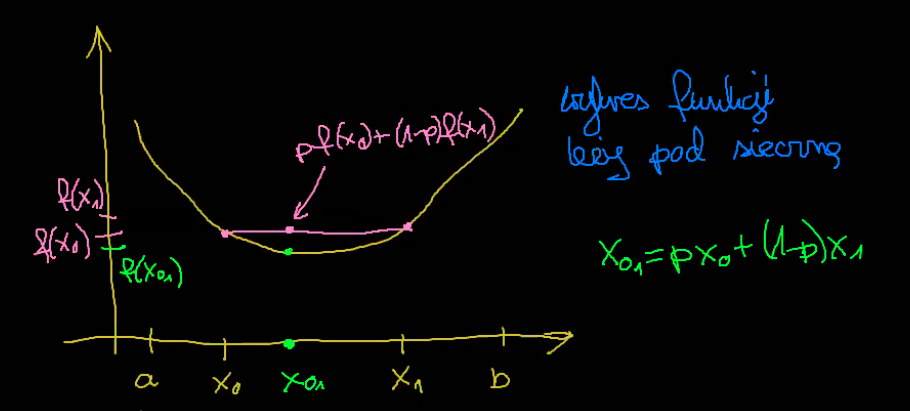
f:[a;b]→R jest wypukła ⟺ gdy ∀x0,x1∈[a;b]∀p∈[0;1] p⋅f(x0)+(1−p)⋅f(x1)≥f(px0+(1−p)x1)
2. DEF: Funkcja ściśle wypukła
∀x0,x1∈[a;b]∀p∈(0;1)
x0=x1 pf(x0)+(1−p)f(x1)>f(px0+(1−p)x1)
3. Fakt#1
(praktyczny)
Jeśli f′′(x)≥0,
to f jest wypukła.
jeśli f′′(x)>0
to f jest ściśle wypukła.
3.1. D-d
- f:[a;b]→R
- y,y′ takie, że y<y′
- y′−yf′(y′)−f′(y)=f′′(ξ) dla pewnego ξ∈(y,y′) z twierdzenia Lagrange’a
Zatem y<y′→f′(y)≤f′(y′)
Stąd, dla x0,x1,p∈(0;1)
f(px0+(1−p)x1)−pf(x0)−(1−p)f(x1)=p(f(px0+(1−p)x1)−f(x0))−(1−p)(f(x1)−f(px0+(1−p)x1))=p(px0+(1−p)x1−x0f(px0+(1−p)x1)−f(x0))(1−p)(x1−x0)−(1−p)(x1−px0−(1−p)x1f(x0)−f(px0+(1−p)x1))⋅p⋅(x1−x0)=p(1−p)(x1−x0)(f′(y)−f′(y′))=(∗)
z twierdzenia Langrage’a
dla pewnych y∈(x0;px0+(1−p)x1) oraz y′∈(px0+(1−p)x1;x1) (tu : y′>y)
(∗)≤0
(∗)<0 dla f ściśle wypukłej
4. Przykład
g(x)=∣x∣ jest wypukła, ale nie ma pochodnej (w x=0).
4.1. Ćwiczenie
Zrób g ściśle wypukłą bez drugiej pochodnej.

