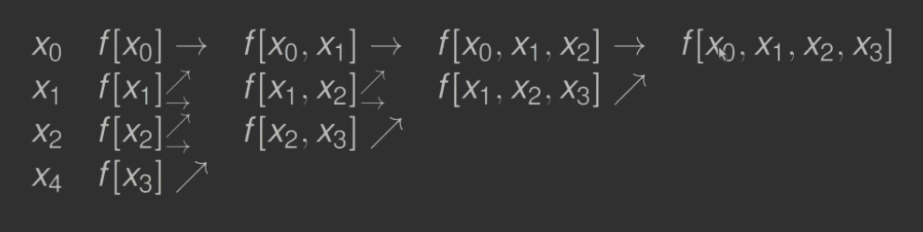Ilorazy różnicowe

• 1. Ilorazy różnicowe
• 2. Postać Newtona wzoru interpolacyjnego
• 3. Twierdzenie o ilorazach różnicowych wyższych rzędów
  • 3.1. D-d
• 4. Sposób uzyskiwania współczynników
  • 4.1. Przykład
• 5. Twierdzenie#4
  • 5.1. D-d
• 6. Twierdzenie#5
  • 6.1. D-d

1. Ilorazy różnicowe

Z Twierdzenie#1 wiemy, że dla różnych węzłów $x_0, x_1, \dots, x_n$ istnieje dokładnie jeden wielomian $p \in \Pi_n$ interpolujący $f$ taki, że $$p(x_i) = f(x_i) \quad (0 \le i \le n).$$

Wielomian $p$ można przedstawić jako kombinację liniową wielomianów $1,x,x^2, \dots, x^n$ (baza $\Pi_n$). Jednak takie przedstawienie nie jest zalecane, ponieważ prowadzi do układu z macierzą Vandermonde’a (zadanie źle uwarnukowane).
Przedstawmy $p$ w innej bazie $\Pi_n$: $$\begin{aligned} q_0(x) &= 1\\ q_1(x) &= (x-x_0)\\ q_2(x) &= (x-x_0)(x-x_1)\\ \dotsb\\ q_n(x) &= (x-x_0) (x - x_1) \dotsb (x - x_{n-1}) \end{aligned}$$

Czyli mamy $$p(x) = \sum_{j=0}^n c_j q_j(x).$$

Z faktu, że $p$ spełnia warunki interpolacji, otrzymujemy układ równań, z którego wyznaczamy $c_0, c_1, \dots, c_n$: $$\sum_{j=0}^n c_j q_j (x_i) = f(x_i) \qquad (0 \le i \le n)$$

Rozwiązując układ z góry w dół wyznaczamy $c_0, c_1, \dots, c_n$. Możemy zauważyć, że

• $c_0$ zależy od $f(x_0)$
• $c_1$ zależy od $f(x_0)$ oraz od $f(x_1)$
• $\dots$
• $c_n$ zależ od $f$ w punktach $x_0, x_1, \dots, x_n$.

Wprowadzimy notację $c_n = f[x_0, x_1, \dots, x_n]$.
$f[x_0,x_1,\dots,x_n]$ jest współczynnikiem przy $q_n$.

Jako, że $$q_n(x) = (x - x_0) (x - x_1) \dotsb (x - x_{n-1}) = x^n + \dotsb$$ więc $f[x_0, x_1, \dots, x_n]$ jest współczynnikiem przy $x^n$ wielomianu stopnia co najwyżej $n$ interpolującego $f$ w węzłach $x_0, x_1, \dots, x_n$. Wielkość $f[x_0, x_1, \dots, x_n]$ będziemy nazywali ilorazem różnicowym opartym na węzłach $x_0, x_1, \dots, x_n$.

Na przykład $f[x_0]$ jest współczynnikiem przy $x^0$ wielomianu stopnia $0$ interpolującego $f$ w $x_0$. $$f[x_0] = f(x_0).$$

$f[x_0, x_1]$ jest współczynnikiem przy $x$ wielomianu stopnia $\le 1$ interpolującego $f$ w $x_0, x_1$. $$p(x) = f(x_0) + \frac{f(x_1) - f(x_0)}{x_1 - x_0} (x - x_0) = f(x_0) + f[x_0, x_1](x - x_0).$$

2. Postać Newtona wzoru interpolacyjnego

Ogólnie $c_i$ wyznaczamy z wcześniejszego układu równań $c_0 = f[x_0], c_1 = f[x_0, x_1]$ aż do $c_n = f[x_0, x_1, \dots, x_n]$.
Otrzymujemy postać Newtona wzoru interpolacyjnego $$p(x) = \sum_{k=0}^n c_k q_k (x) = \sum_{k=0}^n f[x_0, x_1,\dots, x_k] \prod_{j=0}^{k-1} (x - x_j).$$

Oczywiście: $$f[x_i] = f(x_i), \qquad (0 \le i \le n).$$

3. Twierdzenie o ilorazach różnicowych wyższych rzędów

Ilorazy różnicowe spełniają równość: $$f[x_0,x_1,\dots,x_n] = \frac{f[x_1,x_2,\dots,x_n] - f[x_0,x_1,\dots,x_{n-1}]}{x_n - x_0}.$$

3.1. D-d

Niech $p_k \in \Pi_k$ będzie wielomianem interpolującym $f$ w węzłach $x_0, \dots, x_k$. Potrzebujemy wielomianów $p_n$ oraz $p_{n-1}$. Niech będzie wielomianem $q \in \Pi_{n-1}$ interpolującym $f$ w węzłach $x_1,\dots,x_n$.
Wówczas $$p_n(x) = q(x) + \frac{x - x_n}{x_n - x_0} \left( q(x) - p_{n-1}(x) \right)$$

Po obu stronach równości są wielomiany stopnia $\le n$. Wartości tych wielomianów w punktach $x_0, x_1, \dots, x_n$ są takie same, co implikuje wielomiany muszą być identyczne. Potrzeba więc mieć po obu stronach identyczne współczynniki przy $x^n$. Współczynnik wielomianu stopnia $\le n$ interpolującego $f$ w punktach $x_0, x_1, \dots, x_n$ jest równy $f[x_0, x_1, \dots, x_n]$. Stąd dostajemy $$f[x_0, x_1, \dots, x_n] = \frac{f[x_1, x_1,\dots, x_n] - f[x_0, x_1, \dots, x_{n-1}]}{x_n - x_0}$$

4. Sposób uzyskiwania współczynników

Jeżeli dana jest tablica wartości funkcji $(x_i, f(x_i))$, wówczas ilorazy różnicowe łatwo obliczamy konstruując tablicę trójkątną.
Przykład: ilorazy różnicowe rzędów $0,1,2,3$ obliczamy:

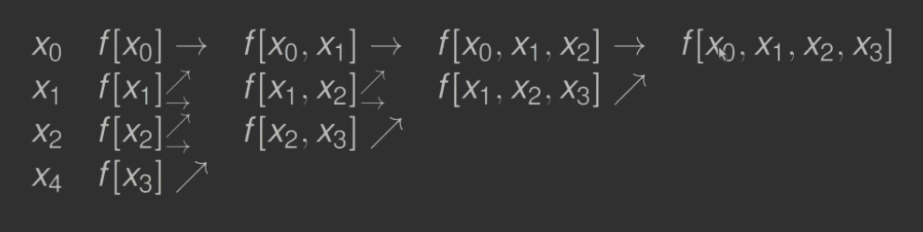
4.1. Przykład

Skonstruować tablicę ilorazów różnicowych dla wartości z tabeli:

Korzystając z Twierdzenia#3 konstruujemy tablicę ilorazów różnicowych

5. Twierdzenie#4

Ilorazy różnicowe nie zależą od kolejności węzłów. Jeśli $(z_0,z_1, \dots, z_n)$ jest permutacją $(x_0, x_1, \dots, x_n)$, to $$f[z_0,z_1,\dots,z_n] = f[x_0,x_1,\dots,x_n].$$

5.1. D-d

Iloraz różnicowy jest równy współczynnikowi przy $x^n$ wielomianu stopnia $\le n$ interpolującego $f$ w węzłach $z_0,z_1,\dots,z_n$. Podobnie iloraz różnicowy $f[x_0,x_1,\dots,x_n]$ jest równy współczynnikowi przy $x^n$ wielomianu stopnia $\le n$ interpolującego $f$ w węzłach $x_0,x_1,\dots,x_n$. Wielomiany oczywiście są równe więc współczynniki są równe.

6. Twierdzenie#5

Niech $p \in \Pi_n$ interpolującym $f$ różnych węzłach $x_0,x_1,\dots,x_n$. Jeżeli $t \neq x_i$, wówczas $$f(t) - p(t) = f[x_0,x_1,\dots,x_n,t] \prod_{j=0}^n (t-x_j).$$

6.1. D-d

Niech $q \in \Pi_{n+1}$ będzie wielomianem interpolującym $f$ w węzłach $x_0,x_1,\dots,x_n,t$. Wielomian $q$ możemy otrzymać z $p$ przez dodanie jednego czynnika (postać Newtona) $$q(x) = p(x) + f[x_0,x_1,\dots,x_n,t] \prod_{j=0}^n (x-x_j).$$

Ponieważ $q(t) = f(t)$ dla $x = t$. Zatem $$f(t) - p(t) = f[x_0,x_1,\dots,x_n,t] \prod_{j=0}^n (t - x_j).$$