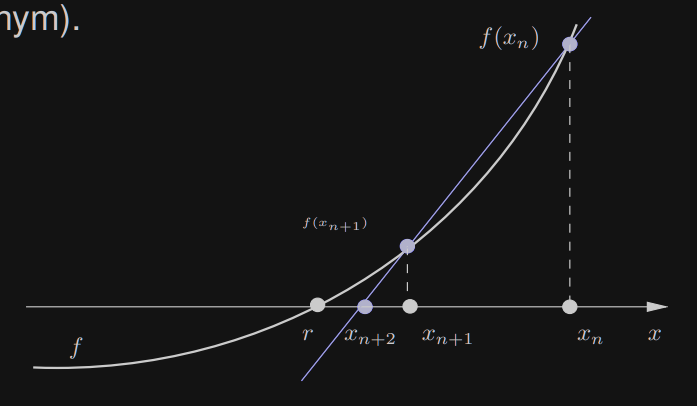
Metoda siecznych

by Jerry Sky

2020-10-20

Metoda siecznych

Założenia:

Aproksymujemy f′(xn)≈f(xn)−f(xn−1)xn−xn−1f'(x_n) \approx \frac{f(x_n) - f(x_{n-1})}{x_n - x_{n-1}}.

xn+1=xn−xn−xn−1f(xn)−f(xn−1)⋅f(xn)=xn+hn x_{n+1} = x_n - \frac{x_n - x_{n-1}}{f(x_n) - f(x_{n-1})} \cdot f(x_n) = x_n + h_n gdzie:

Warunek końca: ∣xn+1−xn∣≤δ|x_{n+1} - x_n| \le \delta, ∣f(xn+1)∣≤ϵ|f(x_{n+1})| \le \epsilon.

Algorytm

  1. fa←f(a)fa \gets f(a)
  2. fb←f(b)fb \gets f(b)
  3. for k←1k \gets 1 to MM:
    1. if ∣fa∣>∣fb∣|fa| > |fb|:
      1. a↔ba \leftrightarrow b
      2. fa↔fbfa \leftrightarrow fb
    2. s←b−afb−fas \gets \frac{b-a}{fb - fa}
    3. b←ab \gets a
    4. fb←fafb \gets fa
    5. a←a−fa⋅sa \gets a - fa \cdot s
    6. fa←f(a)fa \gets f(a)
    7. if ∣b−a∣<δ|b-a| < \delta or ∣fa∣<ϵ|fa| < \epsilon:
      1. return k,a,fak, a, fa

Powyższy algorytm korzysta z funkcji liczącej f(x)f(x).

Twierdzenie o lokalnej zbieżności metody siecznych

Niech f∈C2[a;b]f \in C^2[a;b] i rr będzie jednokrotnym pierwiastkiem ff. Wówczas istnieje otoczenie rr i stała KK i jeśli przybliżenia początkowe x0,x1x_0, x_1 należą do otoczenia rr, to ciąg konstruowanych przez metodę siecznych przybliżeń {xn}\{ x_n \} spełnia ∣xn+1−r∣≤K∣xn−r∣1+52|x_{n+1} - r| \le K|x_n - r|^{\frac{1 + \sqrt{5}}{2}}.

Ponadto lim⁡n→∞xn=r\lim_{n \to \infty} x_n = r.

D-d

Wykładnik zbieżności

Przez błąd rozumiemy wielkość en=xn−re_n = x_n - r.

en+1=xn+1−r=xn−f(xn)f(xn)−f(xn−1)xn−xn−1−r==en−f(xn)f(xn)−f(xn−1)xn−xn−1=en⋅f(xn)−f(xn−1)xn−xn−1−f(xn)f(xn)−f(xn−1)xn−xn−1 e_{n+1} = x_{n+1} - r = x_n - \frac{f(x_n)}{\frac{f(x_n) - f(x_{n-1})}{x_n - x_{n-1}}} - r =\\ = e_n - \frac{f(x_n)}{\frac{f(x_n) - f(x_{n-1})}{x_n - x_{n-1}}} = \frac{e_n \cdot \frac{f(x_n) - f(x_{n-1})}{x_n - x_{n-1}} - f(x_n)}{\frac{f(x_n) - f(x_{n-1})}{x_n - x_{n-1}}}

Funkcję ff można przedstawić za pomocą wzoru interpolacyjnego Newtona f(r)=f(xn)+f(xn)−f(xn−1)xn−xn−1⋅(r−xn)+12f′′(ζn)⋅(r−xn−1)(r−xn)==f(xn)−f(xn)−f(xn−1)xn−xn−1⋅en+12⋅f′′(ζn)⋅en−1⋅en f(r) = f(x_n) + \frac{f(x_n) - f(x_{n-1})}{x_n - x_{n-1}} \cdot (r - x_n) + \frac{1}{2} f''(\zeta_n)\cdot (r - x_{n-1}) (r - x_n) =\\ = f(x_n) - \frac{f(x_n) - f(x_{n-1})}{x_n - x_{n-1}} \cdot e_n + \frac{1}{2} \cdot f''(\zeta_n) \cdot e_{n-1} \cdot e_n

ζn\zeta_n jest liczbą leżącą między xn−1x_{n-1} a xnx_n. 0=f(r)=f(xn)−f(xn)−f(xn−1)xn−xn−1⋅en+12⋅f′′(ζn)⋅en−1⋅en 0 = f(r) = f(x_n) - \frac{f(x_n) - f(x_{n-1})}{x_n - x_{n-1}} \cdot e_n + \frac{1}{2} \cdot f''(\zeta_n) \cdot e_{n-1} \cdot e_n

Przekształcając powyższe równanie otrzymujemy f(xn)−f(xn−1)xn−xn−1⋅en−f(xn)=12⋅f′′(ζn)⋅en−1⋅en \frac{f(x_n) - f(x_{n-1})}{x_n - x_{n-1}} \cdot e_n - f(x_n) = \frac{1}{2} \cdot f''(\zeta_n) \cdot e_{n-1} \cdot e_n

Z twierdzenia o wartości średniej otrzymujemy f′(xn)≈f(xn)−f(xn−1)xn−xn−1=f′(ηn) f'(x_n) \approx \frac{f(x_n) - f(x_{n-1})}{x_n - x_{n-1}} = f'(\eta_n) gdzie ηn\eta_n jest leżącą między xn−1x_{n-1} a xnx_n.

en+1=en⋅f(xn)−f(xn−1)xn−xn−1−f(xn)f(xn)−f(xn−1)xn−xn−1==12f′′(ζn)f′(ηn)⋅en−1⋅en e_{n+1} = \frac{e_n \cdot \frac{f(x_n) - f(x_{n-1})}{x_n - x_{n-1}} - f(x_n)}{\frac{f(x_n) - f(x_{n-1})}{x_n - x_{n-1}}} =\\ = \frac{1}{2} \frac{f''(\zeta_n)}{f'(\eta_n)} \cdot e_{n-1} \cdot e_n

Dla dostatecznie dużych nn jest ζn≈r\zeta_n \approx r, ηn≈r\eta_n \approx r. ∣en+1∣≈12∣f′′(r)f′(r)∣⋅∣en−1∣⋅∣en∣=C⋅∣en−1∣⋅∣en∣ |e_{n+1}| \approx \frac{1}{2} \left| \frac{f''(r)}{f'(r)} \right| \cdot |e_{n-1}| \cdot |e_n| = C\cdot |e_{n-1}| \cdot |e_n|

Twierdzimy, że ∣en+1∣≈K∣en∣p|e_{n+1}| \approx K|e_n|^p

∣en∣≈K∣en−1∣p. |e_n| \approx K|e_{n-1}|^p.

Stąd mamy ∣en−1∣≈∣en∣1p⋅K−1p |e_{n-1}| \approx |e_n|^{\frac{1}{p}} \cdot K^{-\frac{1}{p}}

Dalej ∣en+1∣≈C⋅∣en+1∣⋅∣en∣≈C⋅∣en∣⋅∣en∣1p⋅K−1p=C⋅∣en∣1+1p⋅K−1p |e_{n+1}| \approx C\cdot |e_{n+1}| \cdot |e_n| \approx C\cdot |e_n|\cdot |e_n|^{\frac{1}{p}} \cdot K^{-\frac{1}{p}} = C\cdot |e_n|^{1 + \frac{1}{p}} \cdot K^{-\frac{1}{p}}

Przyrównując stronami K⋅∣en∣p≈C⋅∣en∣1+1p⋅K−1p K\cdot |e_n|^p \approx C\cdot |e_n|^{1 + \frac{1}{p}} \cdot K^{-\frac{1}{p}}

Po pogrupowaniu otrzymujemy K1+1p⋅∣en∣p≈C⋅∣en∣1+1p K^{1 + \frac{1}{p}} \cdot |e_n|^p \approx C \cdot |e_n|^{1+\frac{1}{p}}

Z powyższej równości dostajemy p=1+1pp = 1 + \frac{1}{p}. Dodatnim pierwiastkiem równanie jest p=1+52p = \frac{1 + \sqrt{5}}{2}. Wyznaczamy KK z równania K1+1p=CK^{1 + \frac{1}{p}} = C.
Z faktu, że 1+1p=p1 + \frac{1}{p} = p otrzymujemy równanie Kp=CK^p = C. Ostatecznie K=C1pK = C^{\frac{1}{p}} oraz ∣en+1∣≤K⋅∣en∣1+52. |e_{n+1}| \le K\cdot |e_n|^{\frac{1 + \sqrt{5}}{2}}.

Zbieżność

Jak dla metody Newtona.

■\blacksquare