Metoda bisekcji

by Jerry Sky

2020-10-22

1. Metoda bisekcji (połowienia)

Założenia:

cn=12(an+bn)(n≥0) c_n = \frac{1}{2} (a_n + b_n) \quad (n\ge 0)

Warunek końca: ∣bn−an∣≤δ|b_n - a_n| \le \delta, ∣f(cn)∣≤ϵ|f(c_n)| \le \epsilon

2. Algorytm

  1. u←f(a)u \gets f(a)
  2. v←f(b)v \gets f(b)
  3. e←b−ae \gets b - a
  4. if sgn⁡(u)=sgn⁡(v)\operatorname{sgn}(u) = \operatorname{sgn}(v):
    1. return error
  5. for k←1k \gets 1 to MM:
    1. e←e2e \gets \frac{e}{2}
    2. c←a+ec \gets a + e
    3. w←f(c)w \gets f(c)
    4. if ∣e∣<δ|e| < \delta or ∣w∣<ϵ|w| < \epsilon:
      1. return k,c,wk,c,w
    5. if sgn⁡(w)≠u⁡\operatorname{sgn}(w) \neq \operatorname{u}:
      1. b←cb \gets c
      2. v←wv \gets w
    6. else
      1. a←ca \gets c
      2. u←wu \gets w

3. Twierdzenie o zbieżności metody bisekcji

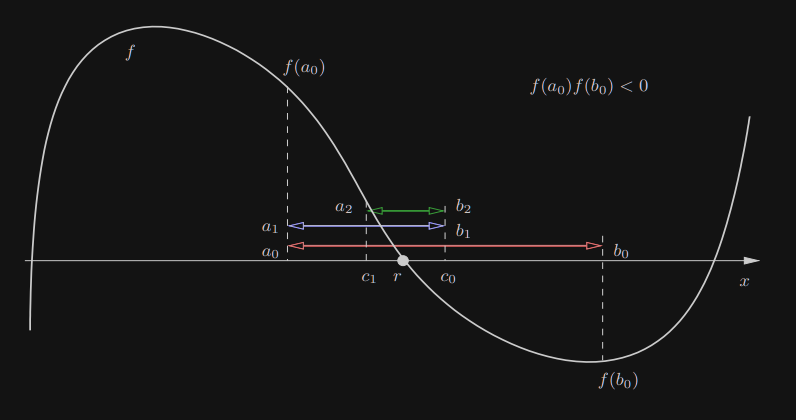
Niech [a0,b0];[a1,b2];… ;[an,bn];…[a_0, b_0]; [a_1, b_2]; \dots; [a_n, b_n]; \dots będzie ciągiem przedziałów konstruowanych przez metodę bisekcji. Wówczas istnieją granice lim⁡n→∞an\lim_{n \to \infty} a_n oraz lim⁡n→∞bn\lim_{n \to \infty} b_n i są sobie równe, reprezentujące zero rr funkcji ff.

Jeśli r=lim⁡n→∞cnr = \lim_{n \to \infty} c_n oraz cn=12(an+bn)c_n = \frac{1}{2}(a_n + b_n), wówczas ∣r−cn∣≤2−(n+1)(b0−a0). |r - c_n| \le 2^{-(n+1)} (b_0 - a_0).

3.1. D-d

Końce generowanych przedziałów spełniają zależności a0≤a1≤a2≤⋯≤b0b0≥b1≥b2≥⋯≥a0 a_0 \le a_1 \le a_2 \le \dotsb \le b_0\\ b_0 \ge b_1 \ge b_2 \ge \dotsb \ge a_0\\

bn−an=12(bn−1−an−1)=2−n(b0−a0) b_n - a_n = \frac{1}{2}(b_{n-1} - a_{n-1}) = 2^{-n} (b_0 - a_0)

Ponieważ ciąg {an}\{ a_n \} (odp. {bn}\{ b_n \}) jest rosnący (odp. malejący) i ograniczony z góry (odp. dołu), więc zbieżny.
Zatem lim⁡n→∞bn−lim⁡n→∞an=lim⁡n→∞2−n(b0−a0)=0 \lim_{n \to \infty} b_n - \lim_{n \to \infty} a_n = \lim_{n \to \infty} 2^{-n} (b_0 - a_0) = 0

Stąd lim⁡n→∞bn=lim⁡n→∞an=r\lim_{n \to \infty} b_n = \lim_{n \to \infty} a_n = r. Przechodząc do granicy w nierówności 0≥f(an)⋅f(bn)0 \ge f(a_n) \cdot f(b_n), otrzymujemy 0≥(f(r))20 \ge \left( f(r) \right)^2. Co implikuje f(r)=0f(r) = 0 (zbieżność).
Niech [an,bn][a_n, b_n] będzie przedziałem wygenerowanym przez metodę bisekcji. Jeśli warunek końca jest już spełniony, oczywiście r∈[an,bn]r \in [a_n, b_n], wówczas najlepszym przybliżeniem pierwiastka rr jest środek przedziału cn=an+bn2c_n = \frac{a_n + b_n}{2}.
Błąd możemy oszacować następująco: ∣r−cn∣≤12(bn−an)=2−(n+1)(b0−a0)■ |r - c_n| \le \frac{1}{2} (b_n - a_n) = 2^{-(n+1)} (b_0 - a_0) \quad \blacksquare

3.2. Przykład

Niech [50,63][50, 63] będzie przedziałem, w którym ff ma pierwiastek.
Jaka jest liczba iteracji metody bisekcji, aby wyznaczyć pierwiastek z błędem względnym 10−1210^{-12}? ∣r−cn∣∣r∣≤∣r−cn∣50≤2−(n+1)1350≤10−12 \frac{|r - c_n|}{|r|} \le \frac{|r - c_n|}{50} \le 2^{-(n+1)} \frac{13}{50} \le 10^{-12}

Rozwiązując powyższą nierówność otrzymujemy n≥37n \ge 37.