Numeryczna niestabilność

by Jerry Sky

2020-10-13

1. Nieformalna definicja

Proces numeryczny jest niestabilny jeśli niewielkie błędy, popełnione w początkowym stadium procesu kumulują się w kolejnych stadiach, powodując poważną utratę dokładności obliczeń.

2. Przykład (ciąg, rekurencja)

Rozważmy ciąg liczb rzeczywistych zdefiniowany za pomocą rekurencyjnego związku: {x0=1x1=13xn+1=133xn−43xn−1(n≥1) \begin{cases} x_0 = 1 \quad x_1 = \frac{1}{3}\\ x_{n+1} = \frac{13}{3}x_n - \frac{4}{3}x_{n-1} & (n \ge 1) \end{cases}

Powyższy związek generuje ciąg xn=(13)nx_n = \left(\frac{1}{3}\right)^n.

Dla n=0n = 0 oraz n=1n = 1 oczywiste.

Załóżmy, że równoważność jest spełniona dla n≤mn \le m. równoważność dla n=m+1n = m+1 wynika 133xm−43xm−1=133(13)m−43(13)m−1=(13)m−1(139−43)=(13)m+1 \frac{13}{3}x_m - \frac{4}{3}x_{m-1} = \frac{13}{3}\left(\frac{1}{3}\right)^m - \frac{4}{3}\left(\frac{1}{3}\right)^{m-1} = \left(\frac{1}{3}\right)^{m-1} \left(\frac{13}{9} - \frac{4}{3}\right) = \left(\frac{1}{3}\right)^{m+1}

Poniżej mamy 15 kolejnych iteracji algorytmu (w arytmetyce single)

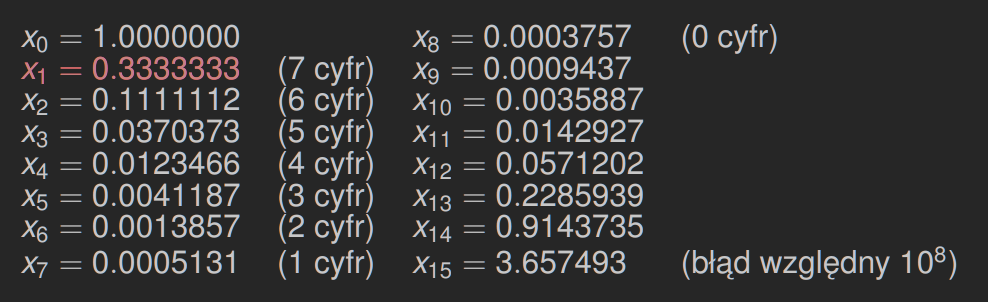
Niedokładność xnx_n przenosi się na xn+1x_{n+1} z mnożnikiem 133\frac{13}{3}. Zatem niedokładność x1x_1, rzędu 10−810^{-8}, przenosi się na x15x_{15} z wielkim mnożnikiem (133)14≈109\left(\frac{13}{3}\right)^{14} \approx 10^9.