Równoważność DFA, NFA oraz RE

• 1. Fakt: Każdy DFA jest NFA
• 2. Twierdzenie#1
  • 2.1. D-d
  • 2.2. Przykład NFA → DFA
• 3. Fakt: Każdy NFA jest NFA$_\epsilon$
• 4. Twierdzenie#2
  • 4.1. D-d
• 5. Twierdzenie#3
  • 5.1. D-d
• 6. Twierdzenie#4
  • 6.1. D-d
  • 6.2. Przykład

1. Fakt: Każdy DFA jest NFA

2. Twierdzenie#1

Niech $L$ będzie językiem akceptowanym przez NFA. Wówczas istnieje DFA akceptujący język $L$.**

2.1. D-d

Niech

• NFA $M = (Q, \Sigma, \delta, q_0, F)$
• DFA $M' = (Q', \Sigma, \delta', q_0', F')$ symulujący równoległe wszystkie przejścia przez automat $M$.

$$\begin{aligned} Q' = 2^Q & \quad \text{śledzimy wszystkie podzbiory stanów} M\\ F' \subseteq Q' &\quad q \in F' \Leftrightarrow \exists p\in q \enspace p\in F\\ q_0' = \{q_0\}\\ \delta'(q,a) &= \bigcup_{p\in q} \delta(p,a) \end{aligned}$$

>Dowód indukcyjny po długości wczytywanego słowa.

2.2. Przykład NFA → DFA

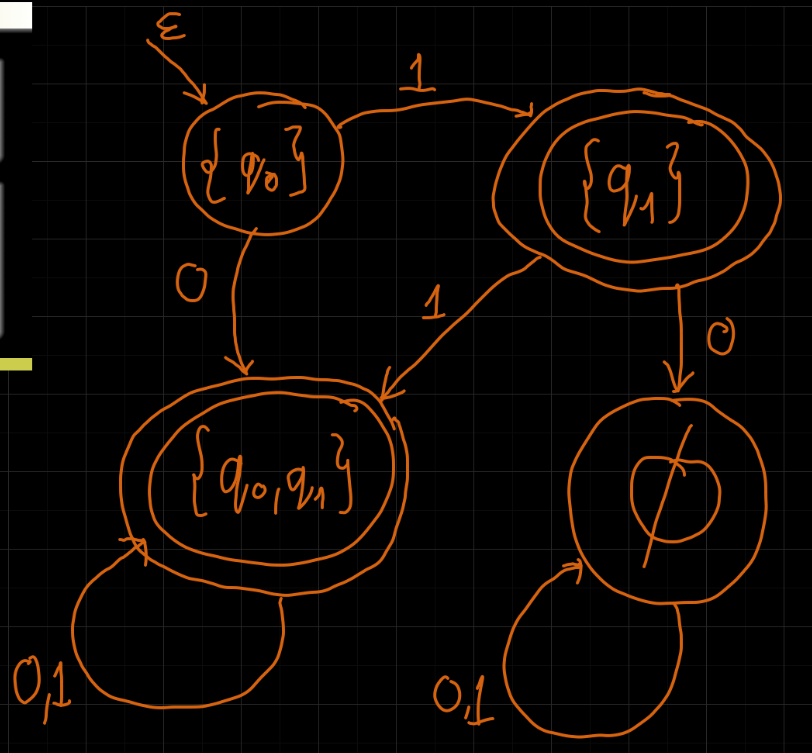
Mamy NFA $M = (\{q_0, q_1\}, \{0,1\}, \delta, q_0, \{q_1\})$ | $\delta$ | $0$ | $1$ | | ——– | ————– | ————– | | $q_0$ | $\{q_0, q_1\}$ | $\{q_1\}$ | | $q_1$ | $\emptyset$ | $\{q_0, q_1\}$ |

Równoważny DFA $M' = \left(\big\{ \{q_0\}, \{q_1\}, \{q_0, q_1\}, \emptyset \big\}, \{0,1\}, \delta', \{q_0\}, \big\{\{q_1\}\big\}\right)$ | $\delta'$ | $0$ | $1$ | | ————– | ————– | ————– | | $\{q_0\}$ | $\{q_0, q_1\}$ | $\{q_1\}$ | | $\{q_1\}$ | $\emptyset$ | $\{q_0, q_1\}$ | | $\{q_0, q_1\}$ | $\{q_0, q_1\}$ | $\{q_0, q_1\}$ | | $\empty$ | $\empty$ | $\empty$ |

3. Fakt: Każdy NFA jest NFA$_\epsilon$

4. Twierdzenie#2

Jeśli $L$ jest językiem akceptowanym przez NFA$_\epsilon$ to jest również akceptowany przez NFA.

4.1. D-d

Niech

• NFA$_\epsilon$ $M = (Q, \Sigma, \delta, q_0, F)$
• NFA $M' = (Q, \Sigma, \delta', q_0, F')$

$$F' = \begin{cases} F \cup \{q_0\} & \text{jeśli z } q_0 \text{ można dojść do } q \in F ~\epsilon\text{-przejściami}\\ F & \text{oth.} \end{cases}$$

$$\delta'(q,a) = \bigcup_{x \in (\epsilon^*a\epsilon^*)}\hat{\delta}(q,x)$$

$M'$ nie ma $\epsilon$-przejść. Równość języków przez dowód indukcyjny po długości słowa.

5. Twierdzenie#3

Niech $r$ będzie wyrażeniem regularnym opisującym język $L$. Wówczas istnieje NFA$_\epsilon$, który akceptuje $L$.

5.1. D-d

Indukcja po budowie wyrażenia regularnego.

• $\emptyset$
• $\epsilon = \{\epsilon\}$
• $\forall a \in \Sigma \enspace a = \{a\}$

$(r+s)$

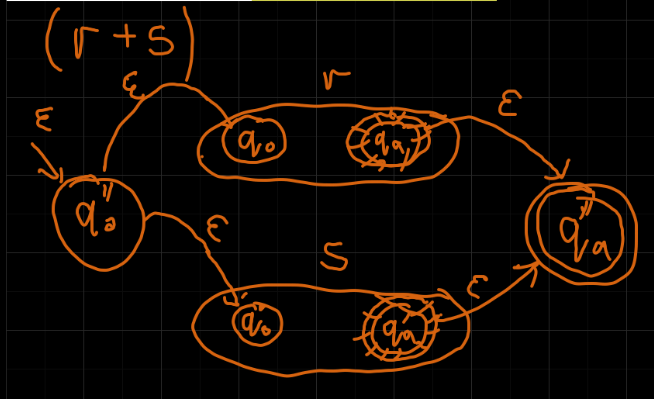
doklejamy nowe stany początkowe i końcowe

$rs$

łączymy w łańcuch

$r^*$

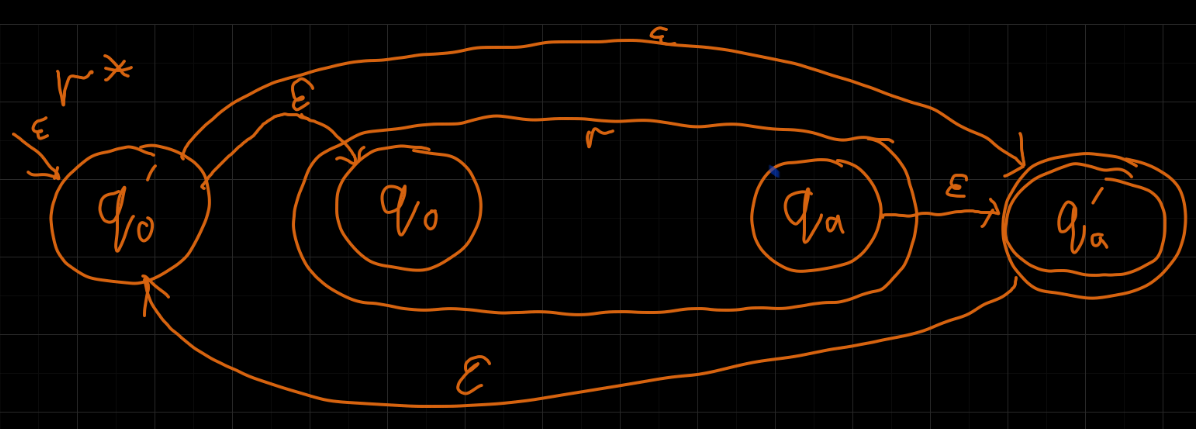
$|r| = n$ jak duży, ile stanów ma automat
$O(n)$

6. Twierdzenie#4

Jeżeli $L$ jest akceptowany przez DFA, to $L$ jest reprezentowany przez wyrażenie regularne.

6.1. D-d

Niech $L$ będzie akceptowany przez DFA $M = (\{ q_1,\dots, q_n \}, \Sigma, \delta, q_1, F)$.

Zdefiniujmy $$R_{ij}^k = \{ x \in \Sigma^*:~ \hat{\delta}(q_i, x) = q_j \land \\ \land~ (\forall y=\mathrm{prefix}(x), y\neq \epsilon, y\neq x)(\hat{\delta}(q_i, y) = q_l \implies l \le k) \}$$

Innymi słowy, $R_{ij}^k$ to zbiór wszystkich słów, z jakimi można przejść ze stanu $q_i$ do stanu $q_j$ używając po drodze tylko pierwszych $k$ stanów ($i,j$ mogą być większe od $k$).
$R_{ij}^k$ — wszystkie łańcuchy, z którymi możemy przejść z $q_i$ do $q_j$.

$$L = \bigcup_{q_j \in F} R_{1j}^n$$

Definicja rekurencyjna: $$R_{ij}^0 = \begin{cases} \{ a:~ \delta(q_1, a) = q_j \} & i \neq j\\ \{ a:~ \delta(q_i, a) = q_i \} \cup \{ \epsilon \} & i = j \end{cases}$$ $R_{ij}^k = R_{ik}^{k-1} \left( R_{kk}^{k-1} \right)^* R_{kj}^{k-1} \cup R_{ij}^{k-1} \quad k>0$

Łatwo skonstruować wyrażenie regularne $r_{ij}^{k}$ opisujące $R_{ij}^k$.

Dowód poprawności przez indukcję po $k$.

6.2. Przykład

~ dla $( \{ q_1, q_2 \}, \{ 0, 1 \},\\ \{ ((q_1, 0), q_1), ((q_1, 1), q_2), ((q_2, 0), q_1), ((q_2, 1), q_2) \}, q_1, \{ q_1 \} )$

$r_{ij}^k = r_{ik}^{k-1} \left( r_{kk}^{k-1} \right)^* r_{kj}^{k-1} + r_{ij}^{k-1} \quad k>0$

$$\begin{aligned} r_{11}^0 &= 0 + \epsilon\\ r_{12}^0 &= 1\\ r_{21}^0 &= 0\\ r_{22}^0 &= 1 + \epsilon\\ r_{11}^1 &= (0 + \epsilon) + (0 + \epsilon)(0 + \epsilon)^* (0 + \epsilon) \equiv 0^*\\ r_{12}^1 &= 1 + (0 + \epsilon)(0 + \epsilon)^* 1 \equiv 0^*1\\ r_{21}^1 &= 0 + 0(0 + \epsilon)^*(0 + \epsilon) \equiv 00^*\\ r_{22}^1 &= (1 + \epsilon) + 0(0 + \epsilon)^* 1 \equiv \epsilon + 0^*1\\ r_{11}^2 &= 0^* + 0^*1(0^*1)^*0^*0 \end{aligned}$$

A tak naprawdę, najprostszym wyrażeniem regularnym dla tego języka jest $\epsilon + (0 + 1)^*0$