Wykład 2020-03-04

for i = 1 to N
  foreach e \in E
    r = $[0,1]
    if r > P(e)
      E = E \ {e}
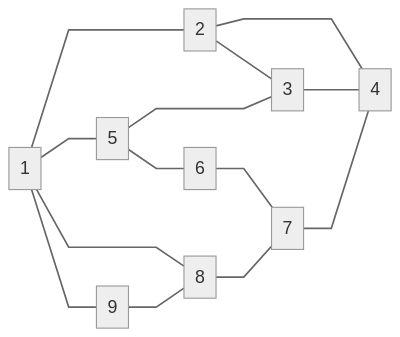
  S = check_connectivity of 'G'
  if S
    success++

$\frac{success}{N}$

for i =1 to {liczba eksperymentów Monte Carlo}

  connectivity of G'

$$N = \begin{array}{c} \begin{matrix} \\ 1 \\ 2 \\ 3 \\ \end{matrix} \begin{array}{r} \begin{matrix} 1 & 2 & 3~~~~~ \end{matrix} \\ \begin{Bmatrix} - & 1 & 2 \\ 1 & - & 3 \\ 2 & 3 & - \end{Bmatrix} \end{array} \end{array}$$

$\frac{success}{liczba eksperymentów Monte Carlo}$

Opóźnienie średnie

$T_{średnie} = \frac{1}{|N|}*\sum\frac{\lambda}{\frac{c}{\mu}-\lambda}$ gdzie

• $\lambda \equiv$ przepływ
• $c \equiv$ przepustowość

???:

• dobierz trasy dla każdej pary wierzchołków
• policz $\lambda_{e}$
• $\lambda_e \ge c_p$

$T_{średnie} \le T_{dopuszczalne}$ - sukces