Pokrycie zbioru

by Jerry Sky

Zobrazowanie
Formalna definicja
Algorytm
- Przykład do algorytmu
Twierdzenie #1
- D-d Twierdzenia #1
Final remarks
More

Zobrazowanie

Problem pokrycia zbioru (set cover) można zobrazować na przykładzie planowania budowy szkół. Powiedzmy, że mamy zbiór wiosek $B$ , w których chcemy zbudować szkoły dla okolicznej młodzieży. Musimy przestrzegać następujących założeń:

każda szkoła musi być w wiosce
odległość, którą muszą przebyć uczniowie do szkoły nie może być większa niż np. 10km.

Celem jest rozmieszczenie szkół w wioskach, aby wszystkie osoby chodzące do szkoły miały ją w odległości nie większej niż ustalona oraz aby wybudować minimalną liczbę szkół. Jeśli dla każdej wioski $x \in B$ zdefiniujemy podzbiór wiosek $S_x \subset B$ będących w odległości mniejszej niż ustalona od $x$ to możemy powiedzieć, że wybudowanie szkoły w wiosce $x$ pokrywa osoby z wiosek należących do zbioru $S_x$ .

Formalna definicja

Input: Zbiór $B$ oraz jego podzbiory $S_1,\dots,S_m \subset B$

Output: Wybór podzbiorów pokrywających zbiór $B$ , czyli $\bigcup_{i\in I}S_i = B$ , gdzie $I$ jest zbiorem indeksów

Koszt: $|I|$ – liczba wybranych podzbiorów

Zależy nam na tym, aby koszt wyborów podzbiorów był jak najmniejszy.

Algorytm

Zauważmy, że zachłanne rozwiązanie samo się tutaj nasuwa:

GreedySetCover $(B, S_1,\dots,S_m)$ :

repeat until $B$ $B$ nie jest całe pokryte:
1. wybierz zbiór $S_i$ , który zawiera najwięcej niepokrytych elementów

Przykład do algorytmu

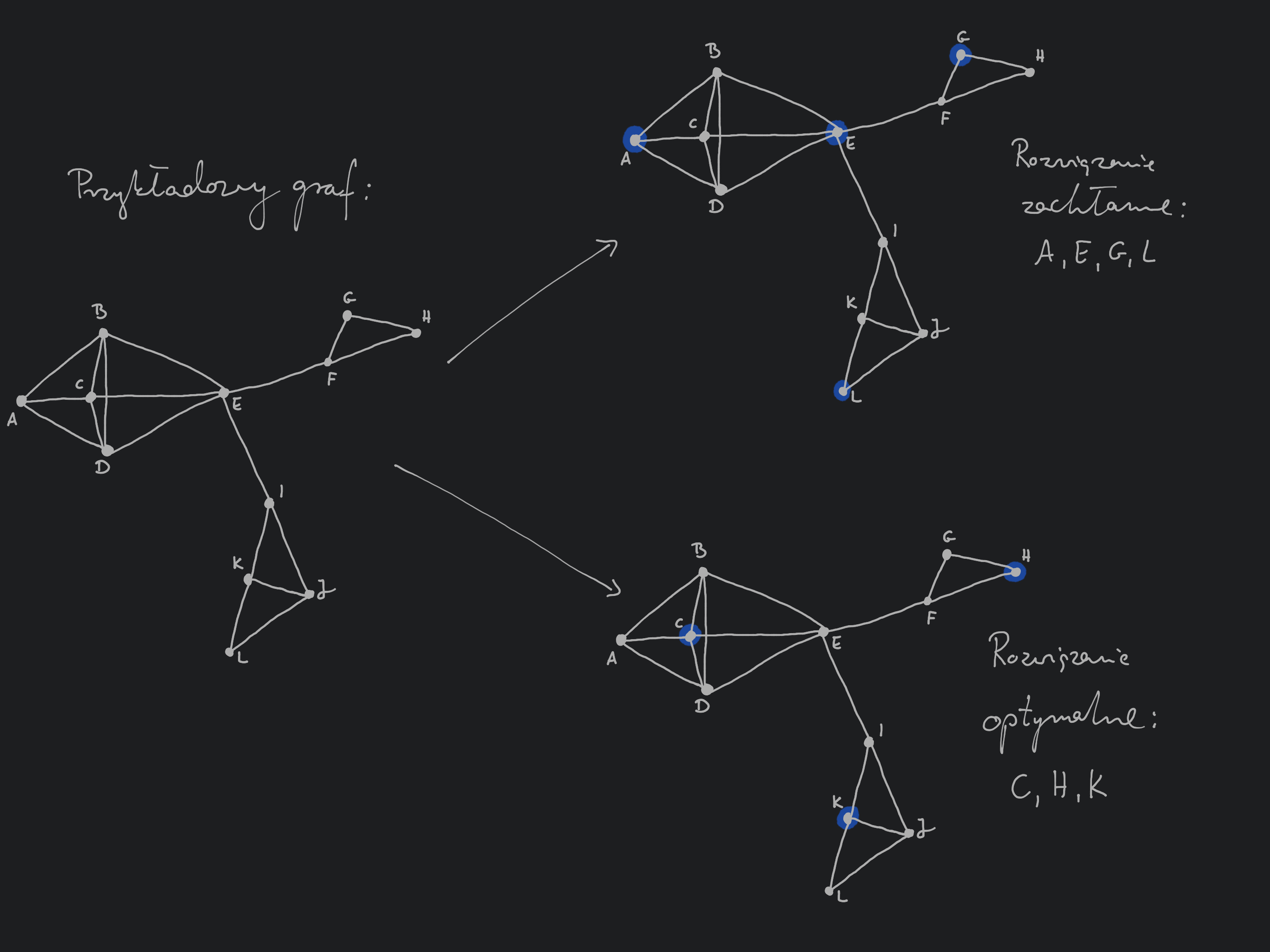
Zobaczmy, jak to naturalne rozwiązanie sprawdza się w praktyce. Wróćmy do naszego przykładu budowy szkół w wioskach. Powiedzmy, że mamy dwunastoelementowy zbiór wiosek: $A,B,C,D,E,F,G,H,I,J,K,L$ . Łączymy ze sobą te wioski, które są oddalone od siebie o mniej niż ustalona wartość:

example

Zatem: $S_A = \{A, B, C, D\}\\ S_B = \{A, B, C, D, E\}\\ S_C = \{A, B, C, D, E\}\\ S_D = \{A, B, C, D, E\}\\ S_E = \{B, C, D, E, F, I\}\\ S_F = \{E, F, G, H\}\\ S_G = \{F, G, H\}\\ S_H = \{F, G, H\}\\ S_I = \{E, I, J, K\}\\ S_J = \{I, J, K, L\}\\ S_K = \{I, J, K, L\}\\ S_L = \{J, K, L\}$

górne rozwiązanie (uzyskane w sposób zachłanny) o koszcie $4$ to $S_A,S_E,S_G,S_L$ , a dolne rozwiązanie o koszcie $3$ (rozwiązanie optymalne) to $S_C,S_H,S_K$ .

Widzimy zatem, że rozwiązanie zachłanne nie musi dawać nam optymalnego rozwiązania. Na szczęście okazuje się, że jesteśmy w stanie ograniczyć odległość rozwiązania zachłannego od optymalnego w zadowalający sposób.

Twierdzenie #1

Załóżmy, że $|B| = n$ , a optymalne rozwiązanie pokrycia zbioru ma koszt $k$ . Wówczas zachłanny algorytm zwróci rozwiązanie o koszcie co najwyżej $k\ln n$ .

D-d Twierdzenia #1

Niech $n_t$ będzie liczbą niepokrytych elementów zbioru $B$ po $t$ iteracjach pętli algorytmu zachłannego $(n_0 = n)$ . Skoro niepokryte elementy da się pokryć optymalnymi $k$ zbiorami to musi istnieć zbiór mający co najmniej $\frac{n_t}{k}$ niepokrytych elementów. Zatem możemy ograniczyć wielkość $n_{t+1}$ przez $n_{t+1} \le n_t - \frac{n_t}{k} = n_t \left( 1 - \frac{1}{k} \right).$

Powtarzając ten argument uzyskujemy ograniczenie: $n_t \le n_0 \left( 1 - \frac{1}{k} \right)^t.$

Użyjmy znanego ograniczenia $\forall x \in \mathbb{R} \setminus \{0\}: 1 - x < e^{-x}$ , które daje nam: $n_t < ne^{-\frac{t}{k}}.$

Zauważmy, że dla $T = k\ln n$ dostajemy $n_T < ne^{-\ln n} = 1$ , co oznacza, że po $k\ln n$ krokach algorytm zachłanny pokryje wszystkie elementy zbioru wejściowego.

Final remarks

Algorytm zachłanny rozwiązujący problem pokrycia zbioru należy do klasy algorytmów aproksymujących (czyli niekoniecznie zwracających optymalne rozwiązanie), a stosunek rozwiązania otrzymanego przy pomocy algorytmu aproksymacyjnego przez rozwiązanie algorytmu optymalnego nazywamy approximation factor. Powyższy algorytm zachłanny dla problemu pokrycia zbioru ma approximation factor równy $ln n$ . Innymi metodami można pokazać również, że nie istnieje algorytm wielomianowy mający mniejszy approximation factor.