Kodowanie Huffmana

• Przykład kompresji MP3
  • Przykładowe kodowanie MP3
  • Niepotrzebne bity
• Zastosowanie kodu Huffmana
  • Pseudokod algorytmu
• More

Przykład kompresji MP3

Schemat kompresji MP3 w sporym uproszczeniu składa się z trzech kroków:

1. Dźwięk jest próbkowany z zadaną częstotliwością (np. 44100 próbek na sekundę) i każda próbka jest opisana przez liczbę rzeczywistą. Otrzymujemy w tens sposób ciąg liczb rzeczywistych: $s_1,\dots,s_T$. Dla przykładu 50 minut muzyki będzie opisane przy pomocy $T = 50 \cdot 60 \cdot 44100 = 132300000$ liczb rzeczywistych (dla uproszczenia zakładamy jeden kanał – dźwięk mono)
2. Każda liczba rzeczywista $s_t$ jest przybliżana przez najbliższą liczbę z ustalonego zbioru $\Gamma$. Zbiór ten jest dobrany w taki sposób, aby jak najlepiej opowiadać ograniczeniom ludzkiego słuchu, a ciąg liczb wykorzystujący wartości ze zbioru $\Gamma$ powinien być nierozróżnialny dla człowieka.
3. Otrzymany ciąg liczb ze zbioru $\Gamma$ o długości $T$ jest zapisywany jako ciągi bitowe.

Przykładowe kodowanie MP3

Przyjrzyjmy się temu ostatniemu krokowi. Powiedzmy, że $\Gamma = \{A,B,C,D\}$ jest czteroelementowym zbiorem. Najprostszy sposób opisania ciągami bitowymi wartości ze zbioru $\Gamma$ będzie nadanie kolejnych dwu-bitowych kodów np. w następujący sposób: $A$ będzie miało kod $00$, $B$ będzie miało kod $01$, $C$ będzie miało kod $10$, a $D$ będzie miało kod $11$. Zatem zapisanie przykładowych 50 minut muzyki będzie wymagało $264.6$ megabitów. Zauważmy, że odczytanie ciągu bitowego odpowiadającego ciągowi wartości ze zbioru $\Gamma$ jest łatwe: czytamy ciąg bitowy od początku do końca biorąc po 2 bity i konwertując je na wartości ze zbioru $\Gamma$.

Niepotrzebne bity

Zastanówmy się, czy da się zapisać interesujący nas ciąg w bardziej efektywny sposób (przy użyciu mniejszej ilości bitów)? Możemy to uczynić posiadając dodatkową informację, np. w postaci częstotliwości występowania w interesującym nas ciągu wartości ze zbioru $\Gamma$. Powiedzmy, że wartość $A$ występuje $3000000$ razy, $B$ występuje $72200000$ razy, $C$ występuje $37000000$ razy, a $D$ występuje $20100000$ razy.

Idea pozwalająca na lepszą kompresję ciągu polega na tym, że częściej występującej wartości chcemy nadać kod bitowy o mniejszej liczbie bitów, czyli będziemy stosowali kodowanie o zmiennej liczbie bitów.

Zauważmy, że to wiąże się z możliwymi problemami z konwersją ciągu bitowego z powrotem na wartości ze zbioru $\Gamma$. Dla przykładu, jeśli wartości $B$ nadamy kod $0$ wartości $C$ kod $1$, a wartości $A$ kod $01$ i otrzymamy ciąg $001$ to nie jesteśmy w stanie stwierdzić, czy to jest zapis ciągu $BBC$, czy może $BA$?
Rozwiązaniem tego problemu są kody prefiksowe, czyli takie, że żaden kod nie jest prefiksem innego kodu.

Zastosowanie kodu Huffmana

Teraz możemy już zdefiniować problem, który znany jest jako kodowanie Huffmana:

Input: tablica częstotliwości $f[1,\dots,n]$ wartości ze zbioru $\Gamma$, gdzie $|\Gamma| = n$.

Output: prefiksowe kody binarne przypisane do wartości ze zbioru $\Gamma$ minimalizujące długość ciągu bitowego odpowiadającemu ciągowi o wejściowych częstotliwościach.

Zauważmy, że ukorzenione drzewo binarne (czyli takie, którego węzły mają dwóch potomków lub są liśćmi) może reprezentować kodowanie prefiksowe w następujący sposób:

• liście drzewa odpowiadają kodowanym symbolom ze zbioru $\Gamma$ – dzięki temu, że wykorzystujemy liście drzewa (a nie węzły wewnętrzne) dostajemy kody prefiksowe
• ścieżka od korzenia drzewa do liścia odpowiada kodowi przypisanemu wartości przypisanej do liścia, zakładając że pójście do lewego potomka koduje $0$, a pójście do prawego potomka koduje $1$

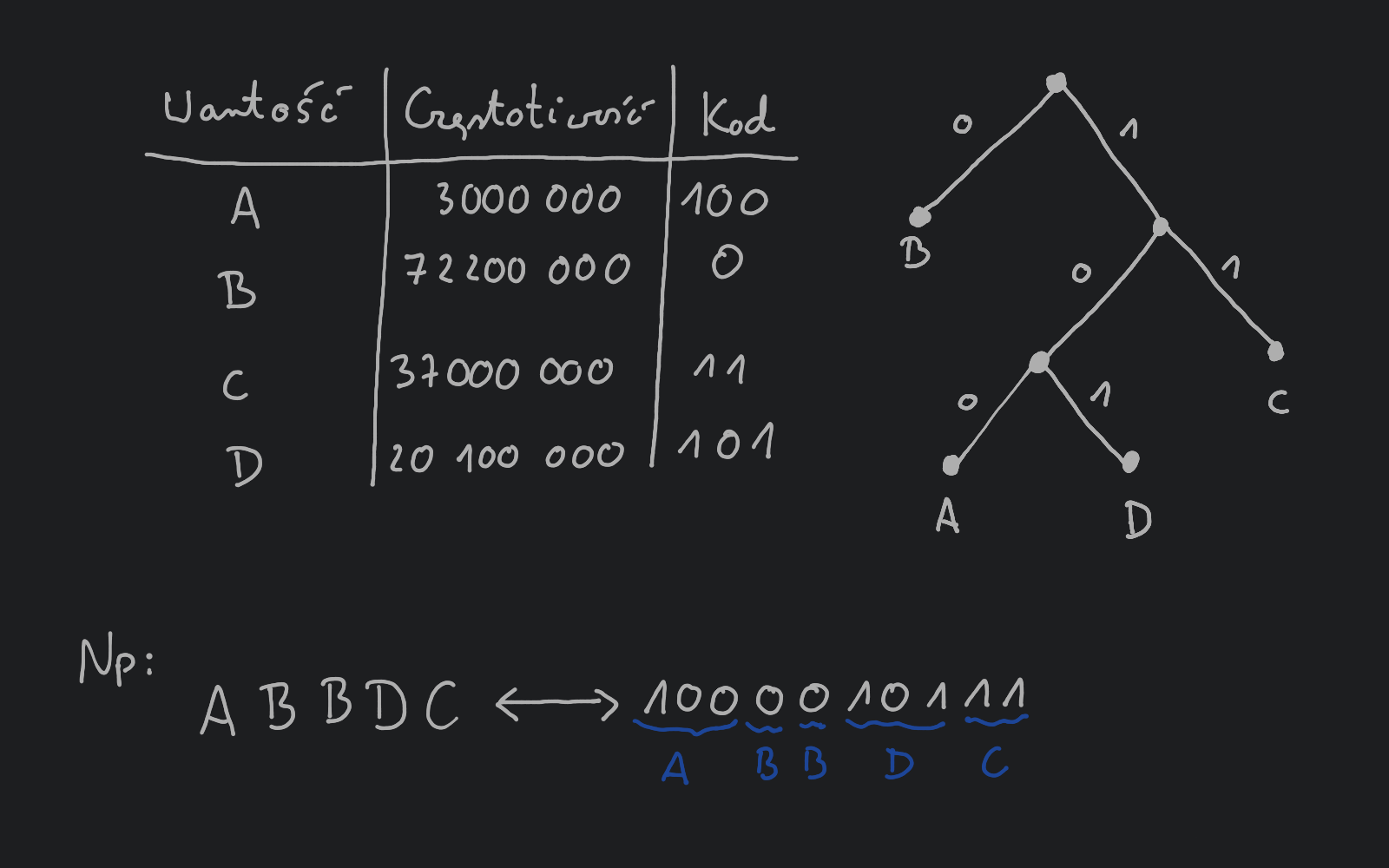
Drzewo kodowe dla wcześniej zaprezentowanego przykładu:

Dla przykładowego drzewa kodowego długość wyjściowego kodu będzie wynosić $3000000 \cdot 3 + 72200000 \cdot 1 + 37000000 \cdot 2 + 20100000 \cdot 3 = 215.5$ megabitów, czyli ponad $18\%$ lepiej niż poprzednio.

Zauważmy, że aby wykonać konwersję kodu binarnego na wartości ze zbioru $\Gamma$ wystarczy przejść wielokrotnie drzewo od korzenia do liścia, tak że jeśli trafimy na $0$ to przechodzimy do lewego potomka, jeśli trafimy na $1$ to przechodzimy do prawego potomka, a jeśli dotrzemy do liścia to zapisujemy odpowiadającą mu wartość.

Formalnie optymalne kodowanie jest takie, które będzie minimalizować długość ciągu binarnego odpowiadającemu ciągowi wartości ze zbioru $\Gamma$, czyli: $$\text{długość kodu całego ciągu} = \\ =\sum_{i=1}^{n} f_i \cdot \text{długość kodu } i\text{-tej wartości ze zbioru } \Gamma$$

Możemy zauważyć, że dla każdej wartości $\alpha \in \Gamma$ długość kodu bitowego odpowiadającego $\alpha$ jest równa głębokości liścia odpowiadającego wartości $\alpha$ w drzewie kodowym. Zatem możemy zapisać długość kodu całego ciągu jako: $$\text{długość kodu całego ciągu} = \\ = \sum_{i=1}^{n} f_i \cdot \text{głębokość liścia odp. } i\text{-tej wartości}$$

Powyższy wzór mówi nam, że dwa symbole z najmniejszą częstotliwością muszą występować w drzewie kodowym, bo w przeciwnym przypadku możemy otrzymać tylko większą długość kodu całego ciągu. Obserwacja ta może być podstawą do pierwszego zachłannego kroku budowy drzewa kodowego.

Zauważmy również, że możemy zdefiniować częstotliwość węzłów wewnętrznych drzewa, która będzie równa sumie częstotliwości potomków danego węzła. Częstotliwość ta odpowiada dokładnie ile razy dany wierzchołek będzie odwiedzony podczas przechodzenia drzewa przy konwersji kodów. Zatem możemy jeszcze inaczej zapisać długość ciągu binarnego na wyjściu: $$\text{długość kodu całego ciągu} = \sum_{v \in T,~ v \neq \mathrm{root}} f_v$$ gdzie $T$ jest drzewem kodowym, $f_v$ jest częstotliwością węzła $v$ należącego do drzewa $T$. Do długości kodu nie dodajemy częstotliwości korzenia drzewa, ponieważ (jak wcześniej zostało to zdefiniowane) przejście krawędzi odpowiada bitowi $0$ lub $1$, więc będąc w korzeniu nie dokładamy bitów do ciągu wyjściowego.

Wykorzystując powyższe obserwacje możemy skonstruować algorytm zachłanny budujący optymalne drzewo kodowe, a co za tym idzie kody binarne przypisane do wartości ze zbioru $\Gamma$ w następujący sposób:

• znajdź dwie wartości ze zbioru $\Gamma$ z najmniejszą częstotliwością (oznaczamy je przez $\alpha,\beta \in \Gamma$, a ich częstotliwości przez $f_1, f_2$), będą one liśćmi i potomkami węzła $v$ o częstotliwości $f_v = f_1 + f_2$
• z trzeciego wzoru na długość ciągu binarnego wiemy, że długość ta będzie równa sumie już użytych częstotliwości $f_1 + f_2$ oraz długości ciągu wynikającego z reszty powstającego drzewa, które teraz będzie miało $n-1$ liści o częstotliwościach $f_v,f_3,f_4,\dots,f_n$.

Pseudokod algorytmu

Huffman$(f[1,\dots,n])$:

1. $\triangleright$ niech $Q$ będzie kolejką priorytetową gdzie priorytetami są częstotliwości; im mniejsza częstotliwość tym większy priorytet
2. for $i \gets 1$ to $n$:
   1. insert$(Q, (i, f[i]))$
3. for $k \gets n+1$ to $2n-1$:
   1. $(i, f[i]) \gets$ ExtractMin$(Q)$
   2. $(j, f[j]) \gets$ ExtractMin$(Q)$
   3. $\triangleright$ stwórz węzeł o indeksie $k$ z potomkami $i$ oraz $j$
   4. $f[k] = f[i] + f[j]$
   5. insert$(Q, (k, f[k]))$

Złożoność obliczeniowa: Używając np. kopca binarnego w celu implementacji kolejki priorytetowej otrzymujemy algorytm o złożoności $O(n\log n)$, bo w pętlach długości $n$ wykonujemy stałą liczbę operacji o złożoności $O(\log n)$.

More

• sekcja 5.2 Algorithms
• sekcja 24 Introduction to Algorithms