Przeszukiwanie wszerz

• BFS$(G, s)$
  • Złożoność obliczeniowa
  • Przykład
• More

BFS$(G, s)$

Mamy graf $G = (V,E,l)$ gdzie $l: E \to \mathbb{R}$ jest funkcją mierzącą długość krawędzi.

Odległością między wierzchołkami $v,u \in V$ nazywamy długość najkrótszej ścieżki pomiędzy $v$ i $u$. Na początek założymy, że wszystkie krawędzie będą miały długość $1$ czyli $\forall_{e \in E}~l(e) = 1$ i będziemy pomijać funkcję $l$ dla uproszczenia.

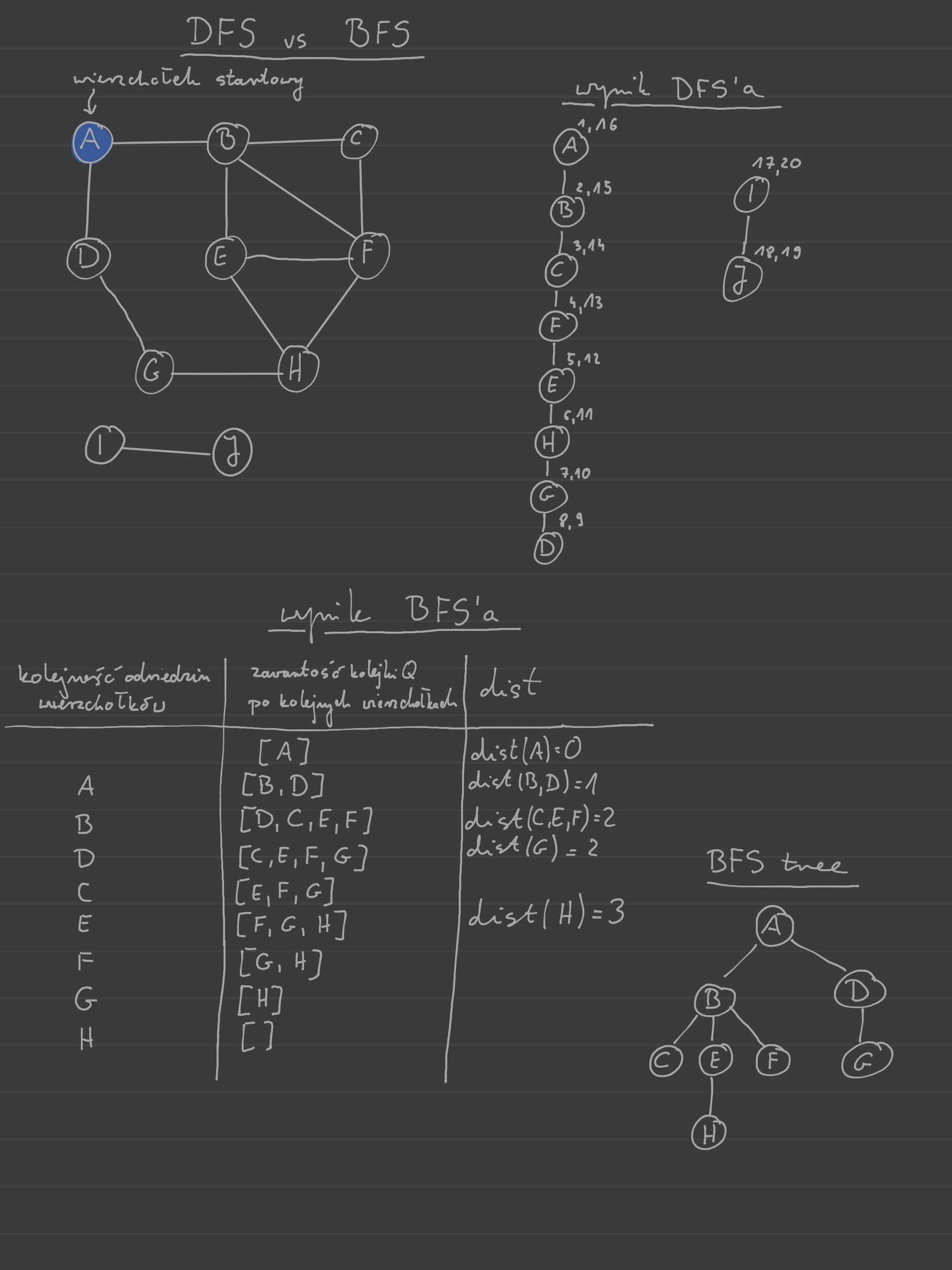
BFS jest procedurą pozwalającą dla grafu $G = (V,E)$ wyznaczyć drzewo najkrótszych ścieżek od wierzchołka startowego $s\in V$. Intuicja stojąca za BFS jest taka, że będziemy przeszukiwać graf warstwa po warstwie, gdzie warstwa będzie rozumiana jako podzbiór wierzchołków w tej samej odległości od wierzchołka startowego $s$.

BFS$(G,s)$:

1. for all $v \in V$:
   1. dist$(v) \gets \infty$
   2. $v.\mathrm{prev} \gets$ null
2. dist$(s) \gets 0$
3. $s.\mathrm{prev} \gets s$
4. $Q \gets [s]$
5. while $|Q| > 0$:
   1. $u \gets Q$.eject$()$
   2. for all $(u,v) \in E$:
      1. if dist$(v) = \infty$:
         1. $Q$.inject$(v)$
         2. dist$(v) \gets$ dist$(u) + 1$
         3. $v.\mathrm{prev} \gets u$

Powyższa procedura na początku inicjuje odległości wszystkich wierzchołków na $\infty$ poza odległością do wierzchołka startowego $s$, która ustalana jest na $0$. Dodatkowo, ustala rodziców węzłów w wynikowym drzewie BFS na null poza węzłem startowym, którego rodzica możemy ustalić na niego samego. Następnie inicjujemy kolejkę FIFO (first in frist out) $Q$, która na początku zawiera tylko wierzchołek startowy $s$. Następnie ściągamy pierwszy wierzchołek z kolejki i sprawdzamy czy odwiedziliśmy już wcześniej jego sąsiadów. Jeśli tak to nic nie robimy, bo oznacza to, że znaleźliśmy do nich krótszą ścieżkę, w przeciwnym przypadku wrzucamy nowo odkryte wierzchołki na koniec kolejki $Q$ i ustawiamy odległość do nich na odległość do wierzchołka, z którego do nich doszliśmy $+1$ oraz ustalamy z jakiego wierzchołka doszliśmy najkrótszą ścieżką do nich. Ustalenie $v.\mathrm{prev}$ pozwala odtworzyć najkrótszą ścieżkę od zadanego wierzchołka do wierzchołka startowego $s$ (czyli w praktyce zbudować wynikowe drzewo BFS).

Zauważmy, że procedura ta spełnia następujące warunki:
$\forall~d = 0,1,2,\dots$ istnieje moment w którym:

• wszystkie węzły grafu $G$ będące w odległości $\le d$ od wierzchołka startowego $s$ mają poprawnie wyznaczoną odległość od $s$
• wszystkie pozostałe węzły grafu $G$ (będące w odległości $> d$ od wierzchołka startowego $s$) mają odległość od $s$ ustawioną na $\infty$
• kolejka $Q$ zawiera jedynie wierzchołki będące w odległości $d$ od wierzchołka startowego $s$

Używając powyższych własności jako założenia indukcyjnego dla ustalonego $d$ możemy łatwo zauważyć, że po ewaluacji wierzchołków będących w kolejce $Q$ (w ostatnim punkcie) przez algorytm, wszystkie te trzy własności zostaną spełnione dla odległości $d+1$. Daje nam to dowód indukcyjny poprawności wyznaczania drzewa najkrótszych ścieżek przez procedurę BFS dla grafu wejściowego $G$ i wierzchołka startowego $s$.

Zauważmy, że jeśli jakiś podzbiór wierzchołków grafu $G$ nie jest dostępny z wierzchołka startowego $s$ to po zakończeniu BFSa wierzchołki te nie zostaną odwiedzone, a odległość do nich pozostanie równa $\infty$.

Złożoność obliczeniowa

• pierwsza pętla przechodzi po wszystkich wierzchołkach, co generuje złożoność $O(|V|)$
• następnie każdy wierzchołek jest jeden raz wkładany do kolejki $Q$ i jeden raz z niej zdejmowany (większość tych operacji dzieje się w pętli while) co daje $2|V|$ operacji na kolejce $Q$
  ponieważ $Q$ jest kolejką FIFO operacja wkładania i zdejmowania elementu na/ z kolejki ma złożoność $O(1)$
• reszta pracy wykonywana jest w pętli for (będącej w pętli while), w której sprawdzana jest każda krawędź (dla grafu skierowanego raz, dla grafu nieskierowanego dwa razy) co generuje złożoność $O(|E|)$
• sumując złożoność procedury BFS wynosi $O(|V| + |E|)$, czyli jest liniowa od wielkości grafu wejściowego $G$.

Przykład

More

• Algorithms DPV~ Chapters 4.1 and 4.2
• CLRS~ Chapter 22.2