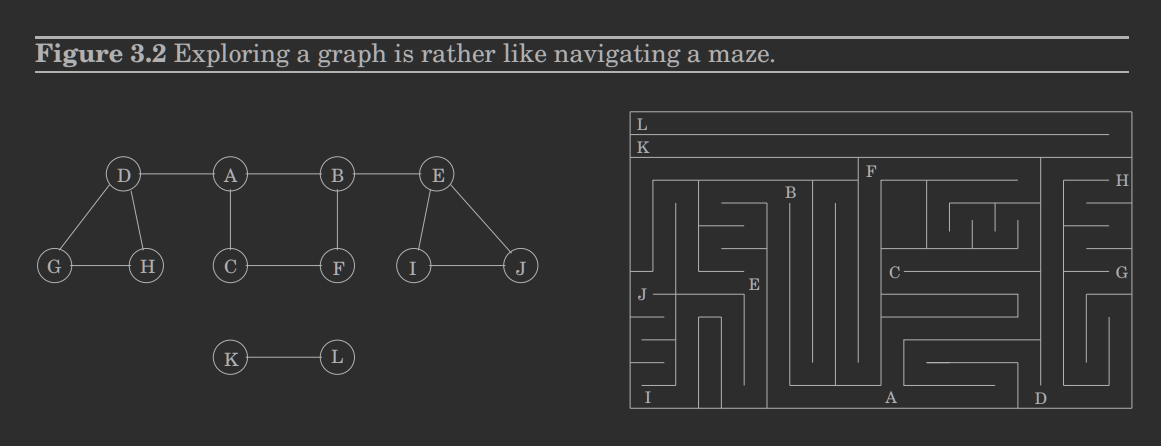
Przeszukiwanie w głąb
DFS grafu nieskierowanego – procedura pozwalająca na eksplorację wszystkich wierzchołków grafu. DFS pozwala odpowiedzieć na pytanie do których wierzchołków grafu można dojść startując z zadanego wierzchołka.
exploreReprezentujemy graf przy pomocy listy sąsiedztwa. Reprezentacja ta pozwala tylko na znajdowanie sąsiadów wierzchołków grafów. Przyjrzyjmy się procedurze explore, która pozwala znaleźć wszystkie wierzchołki grafu dostępne z wierzchołka .
explore:
previsitfor each :
if not :
explorepostvisitProcedur previsit oraz postvisit są opcjonalne i pozwalają na wykonanie operacji w momencie odpowiednio pierwszego odwiedzenia wierzchołka i opuszczenia wierzchołka.
visited jest flagą, która zostanie ustawiona na true dla wszystkich wierzchołków do których można dojść z wierzchołka startowego.
Szkic dowodu poprawności procedury explore można wykonać nie wprost:
visited nie została ustawiona na trueexplore ustawiła flagę visited na trueexplore była w wierzchołku to powinna przejść do wierzchołka .Przykład explore:

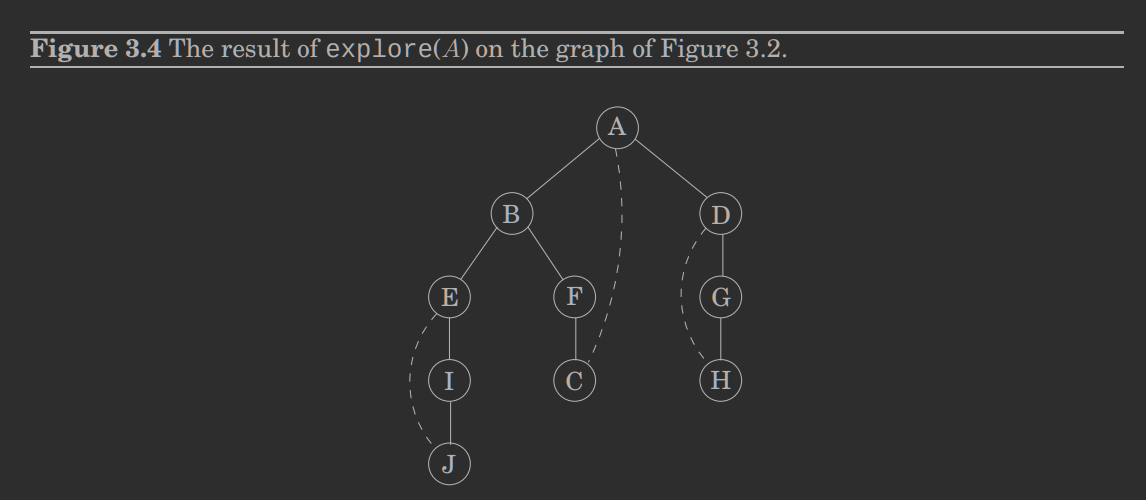
DFSfor all :
visitedfor all :
if not visited:
exploreZłożoność obliczeniowa:
previsit oraz postvisit mamy Pierwszy krok (pętla) sumarycznie dla całego grafu będzie miał złożoność . Drugi krok w każdym wierzchołku ma złożoność obliczeniową zależną od stopnia tego wierzchołka.
Jeśli spojrzymy na to z perspektywy całego grafu to widzimy, że drugi krok przechodzi po każdej krawędzi w grafie dwa razy (dla raz dla explore, drugi raz dla explore).
Zatem złożoność drugiego kroku w całym grafie to . W sumie złożoność obliczeniowa DFS wynosi , czyli liniowo w stosunku do wielkości grafu.
Dodajemy do każdego wierzchołka parametr component_number, zainicjować zmienną cc = 0 na początku procedury DFS, zdefiniować procedurę
previsit:
component_number = ccoraz zwiększać zmienną cc o za każdym razem gdy w procedurze DFS jest procedura explore. Po wykonaniu tak zmodyfikowanego DFSa w zmiennych component_number każdego wierzchołka mamy zapisane, do której komponent należy dany wierzchołek, a zmienna cc zawiera liczbę komponent.