Najkrótsza ścieżka w DAG

• Problem
• Input
• Output
• Remarks
• Pseudocode
• Summary

Problem

Znalezienie najkrótszej ścieżki w skierowanym grafie acyklicznym (DAG).

Input

Graf $G = (V,E,c)$, gdzie:

• $V$ to zbiór wierzchołków grafu
• $E$ to zbiór krawędzi grafu
• $c: E \to \reals$ to funkcja wagi krawędzi
• $v_s \in V$ to wierzchołek startowy ($\mathrm{root}$)

Output

Dla ustalonego wierzchołka startowego $v_s \in V$ długość najkrótszej ścieżki do wszystkich wierzchołków $v_i \in V$ oznaczana przez $d(v_s, v_i)$

Remarks

• Ważną własnością grafu DAG jest możliwość jego „linearyzacji”, czyli ustawienia wierzchołków w takiej kolejności $(v_1, v_2,\dots,v_n)$, że krawędzie będą zawsze skierowane od wcześniejszych wierzchołków do późniejszych $\forall(v_i, v_j) \in E: i<j$.
  
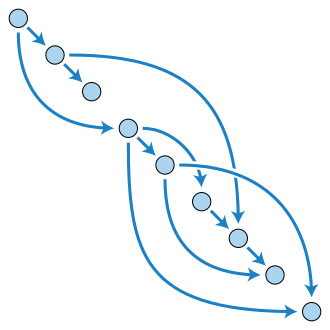
  Dzięki tej własności chcąc policzyć długość najkrótszej ścieżki od wierzchołka startowego $v_s$ do zadanego wierzchołka $v_j$ wystarczy użyć wcześniej obliczonych $d(v_s, v_i)$ dla każdego wierzchołka $(v_i, v_j) \in E$: $$d(v_s, v_j) = \min\{d(v_s,v_i) + c(v_i,v_j): (v_i,v_j) \in E\}$$

• Zauważmy, że każdy wierzchołek odpowiada pod-problemowi, więc jeśli rozwiążemy te pod-problemy od najmniejszych do największych (od pierwszych w ustalonej kolejności do ostatnich) zapamiętując i wykorzystując ich rozwiązania to otrzymamy rozwiązanie problemu znalezienia najkrótszych dróg w DAG.

Pseudocode

for each v in V:
  d(v_s, v) = Infinity
d(v_s, v_s) = 0

for each v in V \ {v_s} in linearized order:
  d(v_s, v) = min{ d(v_s, u) + c(u, v): (u,v) in E }

• Złoż. obli. takiego algorytmu to $O(|E|)$, ponieważ w pętli musimy sprawdzić koszty powstałe dla każdej krawędzi w grafie.
• Zapamiętując dla każdego wierzchołka nie tylko najkrótszą odległość do niego, ale również z którego sąsiada do niego powinniśmy dojść (czyli dla jakiego $u$ osiągamy $\min\{d(v_s, u) + c(u,v): (u,v) \in E\}$) możemy odtworzyć najkrótsze ścieżki w zadanym grafie.

Summary

Problem obliczania najkrótszych ścieżek w DAG leży u podstawy wszystkich algorytmów stworzonych przy użyciu metodologii programowania dynamicznego, ale na ogół DAG nie jest zadany explicite i jednym z zadań jest poprawne go zdefiniowanie.