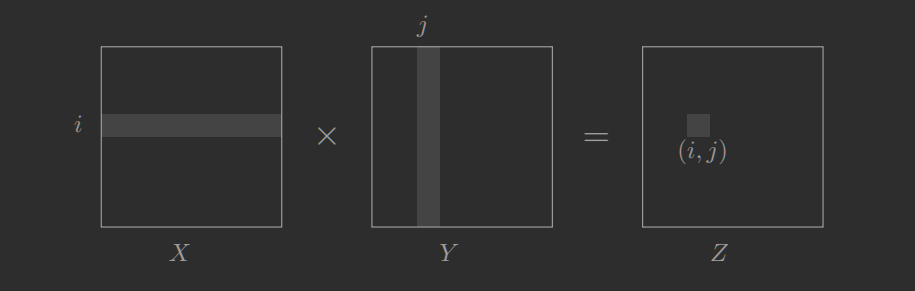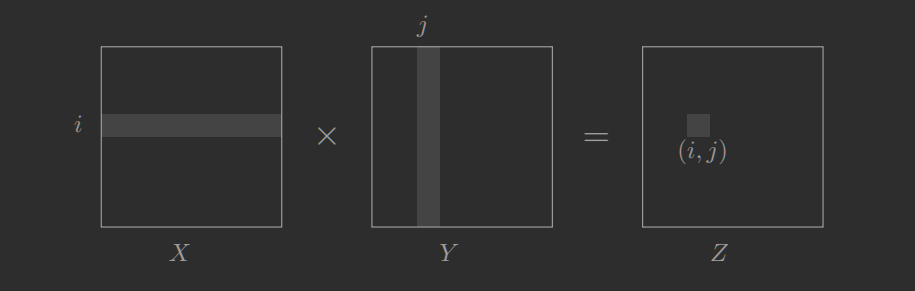Mnożenie macierzy $n\times n$

Strassen

Należy zauważyć, że standardowe podejście do mnożenia macierzy daje algorytm o złożoności obliczeniowej $O(n^3)$.

$X,Y$ - macierze $n\times n$
chcemy $Z = XY$ $$Z_{ij} = \sum_{k=1}^{n}X_{ik}Y_{kj}$$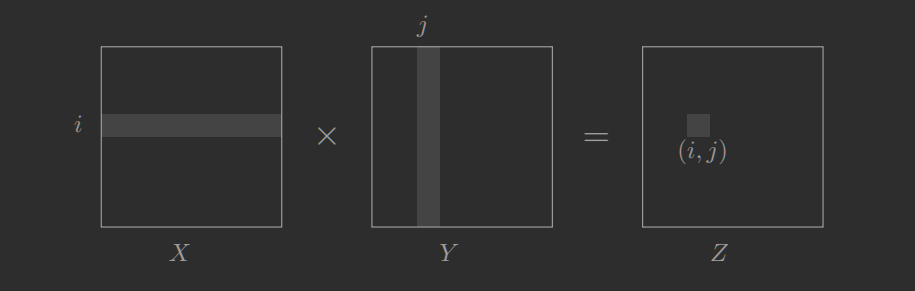

Bezmyślny algorytm typu dziel i zwyciężaj (D&C) również ma złożoność $O(n^3)$. Należy pamiętać, że najważniejsza praca w podejściu D&C dzieje się podczas podziału problemu na mniejsze pod-problemy lub łączenia rozwiązanych pod-problemów.

Algorytm niemieckiego matematyka Volker Strassen’a łączy pod-problemy w zmyślny sposób dzięki czemu ma złożoność $O\big(n^{\log_27}\big)$, gdzie $\log_27 \approx 2.81$.

Mnożenie macierzy jest szczególnie proste do podziału na pod-problemy, np. do podziału na cztery bloki:

$$X = \begin{bmatrix} A & B \\ C & D \end{bmatrix}$$ $$Y = \begin{bmatrix} E & F \\ G & H \end{bmatrix}$$

Wówczas $XY$ jest równe $$\begin{bmatrix} A & B \\ C & D \end{bmatrix} \begin{bmatrix} E & F \\ G & H \end{bmatrix} = \begin{bmatrix} AE + BG & AF + BH \\ CE + DG & CF + DH \end{bmatrix}$$ Nadal mamy złożoność $T(n) = 8 \cdot T\big(\frac{n}{2}\big) + O(n^2) = O(n^3)$.

Jednakże Strassen wpadł na pomysł, dzięki któremu udało się zmniejszyć ilość mnożeń z ośmiu do siedmiu!

$$XY = \begin{bmatrix} P_5 + P_4 - P_2 + P_6 & P_1 + P_2 \\ P_3 + P_4 & P_1 + P_5 - P_3 - P_7 \end{bmatrix}$$ gdzie

• $P_1 = A(F-H)$
• $P_2 = (A+B)H$
• $P_3 = (C+D)E$
• $P_4 = D(G-E)$
• $P_5 = (A+D)(E+H)$
• $P_6 = (B-D)(G+H)$
• $P_7 = (A-C)(E+F)$

Wówczas złożoność obliczeniowa $T(n) = 7\cdot T\big(\frac{n}{2}\big) + O(n^2)$ co dzięki Master Theorem możemy zapisać jako $O\big(n^{\log_27}\big) \approx O\big(n^{2.81}\big)$ co jest znacznie lepszym wynikiem od $O(n^3)$ rzecz jasna.

Source: Algorithms: Dasgupta, Papadimitriou, Vazirani - paragraph 2.5